题目内容
【题目】如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D地边AC上,点E、F在边AB上,点G在边BC上。
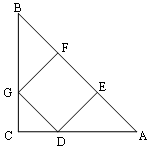
(1)求证:△ADE≌△BGF;
(2)若正方形DEFG的面积为16cm2,求AC的长。
【答案】(1)证明见解析;(2)AC=![]() cm.
cm.
【解析】
试题分析:(1)先根据等腰直角三角形的性质得出∠B=∠A=45°,再根据四边形DEFG是正方形可得出∠BFG=∠AED,故可得出∠BGF=∠ADE=45°,GF=ED,由全等三角形的判定定理即可得出结论;
(2)过点C作CH⊥AB于点H,由正方形DEFG的面积为16cm2可求出其边长,故可得出AB的长,在Rt△ADE中,根据勾股定理可求出AD的长,再由相似三角形的判定定理得出△ADE∽△ACG,由相似三角形的对应边成比例即可求出AC的长.
试题解析:(1)∵△ABC是等腰直角三角形,∠C=90°,
∴∠B=∠A=45°,
∵四边形DEFG是正方形,
∴∠BFG=∠AED=90°,
故可得出∠BGF=∠ADE=45°,GF=ED,
∵在△ADE与△BGF中,
 ,
,
∴△ADE≌△BGF(ASA);
(2)过点C作CH⊥AB于点H,
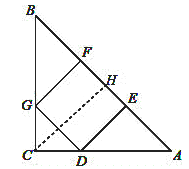
∵正方形DEFG的面积为16cm2,
∴DE=AE=4cm,
∴AB=3DE=12cm,
∵△ABC是等腰直角三角形,CH⊥AB,
∴AH=![]() AB=
AB=![]() ×12=6cm,
×12=6cm,
在Rt△ADE中,
∵DE=AE=4cm,
∴AD=![]() cm,
cm,
∵CH⊥AB,DE⊥AB,
∴CH∥DE,
∴△ADE∽△ACH,
∴![]() ,
,![]() ,
,
解得AC=![]() cm.
cm.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目