题目内容
(2004•济宁)在一次数学活动课上,一位同学提出:“谁能帮我用一副没有刻度的三角板找出线段AB的中点”小华说:“我能做到.我的做法是,用这副三角板任作一条直线MN∥AB;在直线AB、MN的同一侧任取一点P,连接PA、PB,分别交直线MN于C、D;再连接AD、BC,相交于点E;画射线PE交线段AB于点O,点O就是线段AB的中点.”你认为点O是线段AB的中点吗?并说明理由.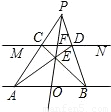
【答案】分析:由于CN∥AB,根据平行线分线段成比例可求出 =
= ,再根据△FDE∽△AOE,即可求出结论.
,再根据△FDE∽△AOE,即可求出结论.
解答:解:∵CN∥AB,
∴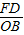 =
= ,
, =
=
∴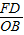 =
=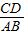
又∵ =
=
∴ =
=
又∵△FDE∽△AOE
∴ =
=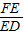
∴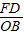 =
=
∴OB=AO.
点评:本题貌似复杂,实质上考查的是平行线分线段成比例定理及相似三角形的性质,是中学阶段的常规题.
 =
= ,再根据△FDE∽△AOE,即可求出结论.
,再根据△FDE∽△AOE,即可求出结论.解答:解:∵CN∥AB,
∴
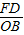 =
= ,
, =
=
∴
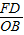 =
=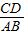
又∵
 =
=
∴
 =
=
又∵△FDE∽△AOE
∴
 =
=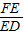
∴
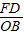 =
=
∴OB=AO.
点评:本题貌似复杂,实质上考查的是平行线分线段成比例定理及相似三角形的性质,是中学阶段的常规题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
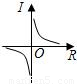
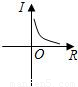
 中,当电压U一定时,电流I与电阻R之间的函数关系可用图象表示为( )
中,当电压U一定时,电流I与电阻R之间的函数关系可用图象表示为( )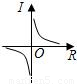
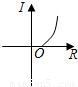


 中,当电压U一定时,电流I与电阻R之间的函数关系可用图象表示为( )
中,当电压U一定时,电流I与电阻R之间的函数关系可用图象表示为( )