题目内容
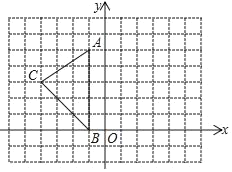
【题目】如图,在平面直角坐标系中,A(﹣1,5)、B(﹣1,0)、C(﹣4,3)
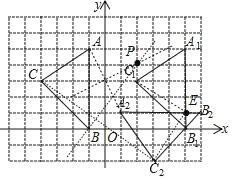
(1)将△ABC向右平移6个单位至△A1B1C1,再将△A1B1C1绕点E(5,1)逆时针旋转90°至△A2B2C2,请按要求画出图形;
(2)在(1)的变换过程中,直接写出点C的运动路径长
(3)△A2B2C2可看成△ABC绕某点P旋转90°得到的,则点P的坐标为 .
【答案】(1)详见解析;(2)6+![]() π;(3)(2,4).
π;(3)(2,4).
【解析】
(1)利用点平移的坐标规律写出![]() 的坐标,然后描点得到△A1B1C1,再利用网格特点和旋转的性质画出
的坐标,然后描点得到△A1B1C1,再利用网格特点和旋转的性质画出![]() 得到△A2B2C2;
得到△A2B2C2;
(2)点C的运动路径长为平移的距离和弧![]() 的长;
的长;
(3)作![]() 和
和![]() 的垂直平分线,它们的交点为P点.
的垂直平分线,它们的交点为P点.
解:(1)如图,△A1B1C1和△A2B2C2为所作;
(2)点C的运动路径长=6+![]() =6+
=6+![]() π;
π;
(3)作![]() 和
和![]() 的垂直平分线,它们的交点为P点,则点P的坐标为(2,4).
的垂直平分线,它们的交点为P点,则点P的坐标为(2,4).
故答案为6+![]() π;(2,4).
π;(2,4).

练习册系列答案
相关题目