题目内容
如图,已知一次函数y1=kx+b与反比例函数 的图象交于A(2,4)、B(﹣4,n)两点.
的图象交于A(2,4)、B(﹣4,n)两点.

(1)分别求出y1和y2的解析式;
(2)写出y1=y2时,x的值;
(3)写出y1>y2时,x的取值范围.
 的图象交于A(2,4)、B(﹣4,n)两点.
的图象交于A(2,4)、B(﹣4,n)两点.
(1)分别求出y1和y2的解析式;
(2)写出y1=y2时,x的值;
(3)写出y1>y2时,x的取值范围.
解:(1)将A(2,4)代入反比例解析式得:m=8,
∴反比例函数解析式为 。
。
将B(﹣4,n)代入反比例解析式得:n=﹣2,即B(﹣4,﹣2)。
将A与B坐标代入一次函数解析式得:
 ,解得:
,解得: 。
。
∴一次函数解析式为y1=x+2。
(2)联立两函数解析式得: ,
,
解得: 或
或 。
。
∴y1=y2时,x的值为2或﹣4。
(3)根据图象和(2)得:y1>y2时,x的取值范围为﹣4<x<0或x>2。
∴反比例函数解析式为
 。
。将B(﹣4,n)代入反比例解析式得:n=﹣2,即B(﹣4,﹣2)。
将A与B坐标代入一次函数解析式得:
 ,解得:
,解得: 。
。∴一次函数解析式为y1=x+2。
(2)联立两函数解析式得:
 ,
,解得:
 或
或 。
。∴y1=y2时,x的值为2或﹣4。
(3)根据图象和(2)得:y1>y2时,x的取值范围为﹣4<x<0或x>2。
试题分析:(1)将A坐标代入反比例解析式中求出m的值,确定出反比例解析式,将B坐标代入反比例解析式求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式。
(2)联立两函数解析式,求出方程组的解即可得到x的值。
(3)由两函数交点坐标,利用图形即可得出所求不等式的解集。

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 向上平移m个单位后,与直线
向上平移m个单位后,与直线 的交点在第一象限,则m的取值范围是
的交点在第一象限,则m的取值范围是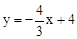 的图象与x轴、y轴分别相交于点A、B.P是射线BO上的一个动点(点P不与点B重合),过点P作PC⊥AB,垂足为C,在射线CA上截取CD=CP,连接PD.设BP=t.
的图象与x轴、y轴分别相交于点A、B.P是射线BO上的一个动点(点P不与点B重合),过点P作PC⊥AB,垂足为C,在射线CA上截取CD=CP,连接PD.设BP=t.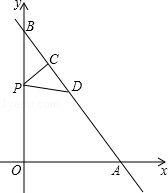

 、
、 在直线
在直线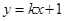 上,且
上,且 ,则该直线所经过的象限是……( )
,则该直线所经过的象限是……( )




 上一点,则点B与其对应点B′间的距离为
上一点,则点B与其对应点B′间的距离为
