题目内容
有一块梯形形状的土地,现要平均分给两个农户种植(即将梯形面积两等分),试设计两种方案,并说明理由.(平分图案画在备用图上,保留作图痕迹)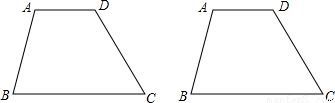
【答案】分析:1、利用两底的中点,将图形分割成两个梯形,它们的上下底分别相等,高也相等,所以面积也相等;
2、连接对角线AC,利用AC的中点E,连接DE和BE,则△ADE的面积=△EDC的面积,△ABE的面积=△BEC的面积,所以ABED和BEDC的面积相等;
解答:解:设梯形上、下底分别为a、b,高为h.
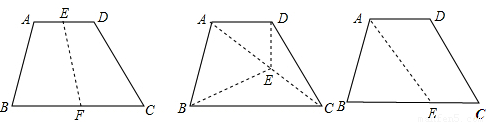
方案一:如图1,连接梯形上、下底的中点E、F,
则S四边形ABFE=S四边形EFCD=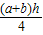 ;
;
方案二:如图2,连接AC,取AC的中点E,连接BE、ED,
则图中的四边形ABED的面积=梯形ABCD的面积的一半,
∵AE=EC,
∴S△ABE=S△BEC,S△AED=S△ECD
∴S△ABE+S△AED=S△BEC+S△ECD,
∴四边形ABED的面积=梯形ABCD的面积的一半.
方案三:如图3,分别量出梯形上、下底a、b的长,在下底BC上截取BE=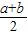 ,连接AE,
,连接AE,
∴S△ABE= BE•h=
BE•h= ,S四边形AECD=S梯形ABCD-S△ABE=
,S四边形AECD=S梯形ABCD-S△ABE=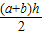 -
-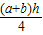 =
=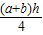 ,
,
则S△ABE=S四边形AECD=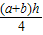 .
.
点评:本题需仔细分析题意,结合图形,利用中点即可解决问题.
2、连接对角线AC,利用AC的中点E,连接DE和BE,则△ADE的面积=△EDC的面积,△ABE的面积=△BEC的面积,所以ABED和BEDC的面积相等;
解答:解:设梯形上、下底分别为a、b,高为h.
方案一:如图1,连接梯形上、下底的中点E、F,
则S四边形ABFE=S四边形EFCD=
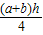 ;
;方案二:如图2,连接AC,取AC的中点E,连接BE、ED,
则图中的四边形ABED的面积=梯形ABCD的面积的一半,
∵AE=EC,
∴S△ABE=S△BEC,S△AED=S△ECD
∴S△ABE+S△AED=S△BEC+S△ECD,
∴四边形ABED的面积=梯形ABCD的面积的一半.
方案三:如图3,分别量出梯形上、下底a、b的长,在下底BC上截取BE=
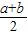 ,连接AE,
,连接AE,∴S△ABE=
 BE•h=
BE•h= ,S四边形AECD=S梯形ABCD-S△ABE=
,S四边形AECD=S梯形ABCD-S△ABE=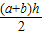 -
-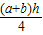 =
=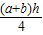 ,
,则S△ABE=S四边形AECD=
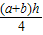 .
.
点评:本题需仔细分析题意,结合图形,利用中点即可解决问题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 19、如图所示,有一块梯形形状的土地,现要平均分给两个农户种植(即将梯形面积等分),试设计一种方案(用尺规作图,保留作图痕迹,不要求写出做法),并简要说明理由.
19、如图所示,有一块梯形形状的土地,现要平均分给两个农户种植(即将梯形面积等分),试设计一种方案(用尺规作图,保留作图痕迹,不要求写出做法),并简要说明理由.