题目内容
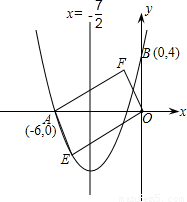
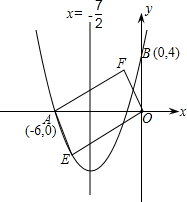
如图,对称轴为直线x=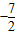 的抛物线经过点A(-6,0)和点B(0,4).
的抛物线经过点A(-6,0)和点B(0,4).(1)求抛物线的解析式和顶点坐标;
(2)设点E(x,y)是抛物线上的一个动点,且位于第三象限,四边形OEAF是以OA为对角线的平行四边形,求?OEAF的面积S与x的函数关系式,并写出自变量x的取值范围;
①当?OEAF的面积为24时,请判断?OEAF是否为菱形?
②是否存在点E,使?OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.•
【答案】分析:(1)根据对称轴设抛物线的解析式为y=a(x+ )2+k,将A、B两点坐标代入,列方程组求a、k的值;
)2+k,将A、B两点坐标代入,列方程组求a、k的值;
(2)根据平行四边形的性质可知S=2S△OAE,△OAE的底为AO,高为E点纵坐标的绝对值,由此列出函数关系式,①当S=24时,由函数关系式得出方程,求x的值,再逐一判断;②不存在,只有当0E⊥AE且OE=AE时,□OEAF是正方形,由此求出E点坐标,判断E点坐标是否在抛物线上.
解答:解:(1)设抛物线的解析式为y=a(x+ )2+k(k≠0),
)2+k(k≠0),
则依题意得: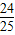 a+k=0,
a+k=0, a+k=4
a+k=4
解之得:a= ,
,
k=-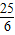
即:y= (x+
(x+ )2-
)2-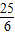 ,顶点坐标为(-
,顶点坐标为(- ,-
,-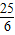 );
);
(2)∵点E(x,y)在抛物线上,且位于第三象限.
∴S=2S△OAE=2× ×0A×(-y)
×0A×(-y)
=-6y
=-4(x+ )2+25 (-6<x<-1);
)2+25 (-6<x<-1);
①当S=24时,即-4(x+ )2+25=24,
)2+25=24,
解之得:x1=-3,x2=-4
∴点E为(-3,-4)或(-4,-4)
当点E为(-3,-4)时,满足OE=AE,故□OEAF是菱形;
当点E为(-4,-4)时,不满足OE=AE,故□OEAF不是菱形.
②不存在.
当0E⊥AE且OE=AE时,□OEAF是正方形,此时点E的坐标为(-3,-3),
而点E不在抛物线上,故不存在点E,使□OEAF为正方形.
点评:本题考查了二次函数的综合运用.关键是根据已知条件求抛物线解析式,根据平行四边形的性质表示面积,由特殊平行四边形的性质确定E点坐标,判断E点坐标是否在抛物线上,确定存在性.
 )2+k,将A、B两点坐标代入,列方程组求a、k的值;
)2+k,将A、B两点坐标代入,列方程组求a、k的值;(2)根据平行四边形的性质可知S=2S△OAE,△OAE的底为AO,高为E点纵坐标的绝对值,由此列出函数关系式,①当S=24时,由函数关系式得出方程,求x的值,再逐一判断;②不存在,只有当0E⊥AE且OE=AE时,□OEAF是正方形,由此求出E点坐标,判断E点坐标是否在抛物线上.
解答:解:(1)设抛物线的解析式为y=a(x+
 )2+k(k≠0),
)2+k(k≠0),则依题意得:
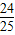 a+k=0,
a+k=0, a+k=4
a+k=4解之得:a=
 ,
,k=-
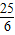
即:y=
 (x+
(x+ )2-
)2-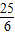 ,顶点坐标为(-
,顶点坐标为(- ,-
,-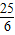 );
);(2)∵点E(x,y)在抛物线上,且位于第三象限.
∴S=2S△OAE=2×
 ×0A×(-y)
×0A×(-y)=-6y
=-4(x+
 )2+25 (-6<x<-1);
)2+25 (-6<x<-1);①当S=24时,即-4(x+
 )2+25=24,
)2+25=24,解之得:x1=-3,x2=-4
∴点E为(-3,-4)或(-4,-4)
当点E为(-3,-4)时,满足OE=AE,故□OEAF是菱形;
当点E为(-4,-4)时,不满足OE=AE,故□OEAF不是菱形.
②不存在.
当0E⊥AE且OE=AE时,□OEAF是正方形,此时点E的坐标为(-3,-3),
而点E不在抛物线上,故不存在点E,使□OEAF为正方形.
点评:本题考查了二次函数的综合运用.关键是根据已知条件求抛物线解析式,根据平行四边形的性质表示面积,由特殊平行四边形的性质确定E点坐标,判断E点坐标是否在抛物线上,确定存在性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•莒南县二模)如图,对称轴为直线x=
(2013•莒南县二模)如图,对称轴为直线x=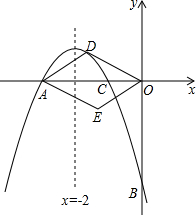 如图,对称轴为直线x=-2的抛物线经过A(-3,0)和B(0,-3).
如图,对称轴为直线x=-2的抛物线经过A(-3,0)和B(0,-3). 如图,对称轴为直线
如图,对称轴为直线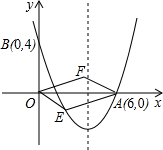 行四边形?若能,求出点E、F的坐标;若不能,请说明理由.(第(4)问不写解答过程,只写结论)
行四边形?若能,求出点E、F的坐标;若不能,请说明理由.(第(4)问不写解答过程,只写结论) 已知如图,对称轴为直线x=4的抛物线y=ax2+2x与x轴相交于点B、O.
已知如图,对称轴为直线x=4的抛物线y=ax2+2x与x轴相交于点B、O.