Question

【题目】如图，点O为原点，A. B为数轴上两点，AB=15，且OA:OB=2.

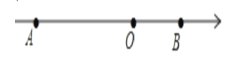
(1)A、B对应的数分别为___、___；

(2)点A. B分别以4个单位/秒和3个单位/秒的速度相向而行，则几秒后A. B相距1个单位长度?

(3)点A. B以(2)中的速度同时向右运动，点P从原点O以7个单位/秒的速度向右运动，是否存在常数m，使得4AP+3OBmOP为定值，若存在请求出m值以及这个定值；若不存在，请说明理由。

Answer 1

【答案】（1）A、B对应的数分别为10、5；（2）2或秒；（3）当m=3时，4AP+3OBmOP为定值55.

【解析】

（1）根据题意求出OA、OB的长，根据数轴的性质解答；

（2）分点A在点B的左侧、点A在点B的右侧两种情况，列方程解答；

（3）根据题意列出关系式，根据定值的确定方法求出m即可．

(1)设OA=2x，则OB=x，

由题意得，2x+x=15，

解得，x=5，

则OA=10、OB=5，

∴A、B对应的数分别为10、5，

故答案为：10；5；

(2)设x秒后A. B相距1个单位长度，

当点A在点B的左侧时，4x+3x=151，

解得，x=2，

当点A在点B的右侧时，4x+3x=15+1，

解得,x=，

答：2或秒后A. B相距1个单位长度；

(3)设t秒后4AP+3OBmOP为定值，

由题意得,4AP+3OBmOP=4×[7t(4t10)]+3(5+3t)7mt

=(217m)t+55，

∴当m=3时，4AP+3OBmOP为定值55.