题目内容
【题目】如图,直线OB是一次函数y=2x的图象,点A的坐标是(0,2),点C在直线OB上且△ACO为等腰三角形,求C点坐标.
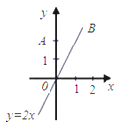
【答案】(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(-
),(-![]() ,-
,-![]() ),C4(
),C4(![]() ,1)
,1)
【解析】试题分析:本题要分三种情况进行讨论,
第一种情况:以OA为腰,A为等腰三角形的顶点,那么C点必定在第一象限,且纵坐标的值比A的要大,根据OA=AC我们知道了AC的距离,我们可以根据C的纵坐标和横坐标以及AC的长构成的直角三角形,运用勾股定理以及所在直线的函数关系式求出C的坐标.
第二种情况:以OA为一腰,O为三角形的顶点,那么C点可以有两个,一个在第一象限,一个在第三象限,且这两个点关于原点对称.我们只要求出一个两个就都求出来了,求的方法同第一种情况.
第三种情况:以OA为底,OC,AC为腰,此点在第一象限,那么这点的纵坐标必为1(顶点在底边的垂直平分线上),那么根据所在函数的关系式,可求出这个C点的坐标.
试题解析:如图,
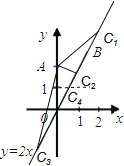
若此等腰三角形以OA为一腰,且以A为顶点,则AO=AC1=2.
设C1(x,2x),则得x2+(2x-2)2=22,
解得x=![]() ,得C1(
,得C1(![]() ,
, ![]() ),
),
若此等腰三角形以OA为一腰,且以O为顶点,则OC2=OC3=OA=2,
设C2(x′,2x′),则得x′2+(2x′)2=22,解得x′=![]() ,
,
∴C2(![]() ,
, ![]() ),
),
又由点C3与点C2关于原点对称,得C3(![]() ,
,![]() ),
),
若此等腰三角形以OA为底边,则C4的纵坐标为1,从而其横坐标为![]() ,得C4(
,得C4(![]() ,1),
,1),
所以,满足题意的点C有4个,坐标分别为:(![]() ,
, ![]() ),(
),(![]() ,
, ![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,1).
,1).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



