题目内容
如图:(1)试验观察: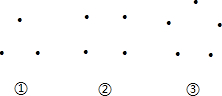
如果每过两点可以画一条直线,那么:
第①组最多可以画
第②组最多可以画
第③组最多可以画
(2)探索归纳:
如果平面上有n(n≥3)个点,且每3个点均不在1条直线上,那么最多可以画
条直线.(用含n的代数式表示)
(3)解决问题:
某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握

如果每过两点可以画一条直线,那么:
第①组最多可以画
3
3
条直线;第②组最多可以画
6
6
条直线;第③组最多可以画
10
10
条直线.(2)探索归纳:
如果平面上有n(n≥3)个点,且每3个点均不在1条直线上,那么最多可以画
| n(n-1) |
| 2 |
| n(n-1) |
| 2 |
(3)解决问题:
某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握
990
990
次手.分析:(1)根据图形画出直线即可;
(2)根据上面得到的规律用代数式表示即可;
(3)将n=45代入即可求解.
(2)根据上面得到的规律用代数式表示即可;
(3)将n=45代入即可求解.
解答:解:(1)根据图形得:如图:(1)试验观察
如果每过两点可以画一条直线,那么:
第①组最多可以画3条直线;
第②组最多可以画6条直线;
第③组最多可以画10条直线.
(2)探索归纳:
如果平面上有n(n≥3)个点,且每3个点均不在1条直线上,那么最多可以画1+2+3+…+n-1=
条直线.(用含n的代数式表示)
(3)解决问题:
某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握990次手.
如果每过两点可以画一条直线,那么:
第①组最多可以画3条直线;
第②组最多可以画6条直线;
第③组最多可以画10条直线.
(2)探索归纳:
如果平面上有n(n≥3)个点,且每3个点均不在1条直线上,那么最多可以画1+2+3+…+n-1=
| n(n-1) |
| 2 |
(3)解决问题:
某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握990次手.
点评:本体考查了图形的变化类问题,解题的关键是仔细的观察图形并找到其中的规律.

练习册系列答案
相关题目