题目内容
某商店购进一种单价30元的T恤.试销中发现这种T恤每天的销售量p(件)与每件的销售价x(元)满足一次函数关系:p=ax+b,部分对应关系如下表:| x | … | 31 | 32 | 33 | 34 | 35 | … |
| p | … | 38 | 36 | 34 | … |
(2)求销售量p(件)与每件的销售价x(元)之间的函数解析式;
(3)试问:销售价x定为多少元时?每天获得的利润最大.
【答案】分析:(1)根据图表可以得出数据变化规律,依次减2得出答案即可;
(2)根据已知条件求出该商店每天的销售量p(件)与每件的销售价x(元)之间的函数关系,
(3)表示出每天销售这种商品的利润,根据题意列出函数关系式即可求出.
解答:解:(1)根据图表可以得出数据变化规律:
∴答案为:32;30;
(2)假设一次函数关系式为:p=kx+b,
∴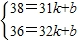 ,
,
解得: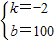 ,
,
∴p=-2x+100;
(3)根据题意得出:
y=(-2x+100)(x-30)=-2x2+160x-3000,
当x=40时,y最大=2900元.
点评:此题主要考查了二次函数与一次函数的应用,列出一次函数的解析式和二次函数解析式是解题关键.
(2)根据已知条件求出该商店每天的销售量p(件)与每件的销售价x(元)之间的函数关系,
(3)表示出每天销售这种商品的利润,根据题意列出函数关系式即可求出.
解答:解:(1)根据图表可以得出数据变化规律:
∴答案为:32;30;
(2)假设一次函数关系式为:p=kx+b,
∴
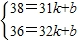 ,
,解得:
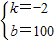 ,
,∴p=-2x+100;
(3)根据题意得出:
y=(-2x+100)(x-30)=-2x2+160x-3000,
当x=40时,y最大=2900元.
点评:此题主要考查了二次函数与一次函数的应用,列出一次函数的解析式和二次函数解析式是解题关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
某商店购进一种单价30元的T恤.试销中发现这种T恤每天的销售量p(件)与每件的销售价x(元)满足一次函数关系:p=ax+b,部分对应关系如下表:
| x | … | 31 | 32 | 33 | 34 | 35 | … |
| p | … | 38 | 36 | 34 | … |
(2)求销售量p(件)与每件的销售价x(元)之间的函数解析式;
(3)试问:销售价x定为多少元时?每天获得的利润最大.
某商店购进一种单价30元的T恤.试销中发现这种T恤每天的销售量p(件)与每件的销售价x(元)满足一次函数关系:p=ax+b,部分对应关系如下表:
(1)请补全上表中的两个空格;
(2)求销售量p(件)与每件的销售价x(元)之间的函数解析式;
(3)试问:销售价x定为多少元时?每天获得的利润最大.
| x | … | 31 | 32 | 33 | 34 | 35 | … |
| p | … | 38 | 36 | 34 | … |
(2)求销售量p(件)与每件的销售价x(元)之间的函数解析式;
(3)试问:销售价x定为多少元时?每天获得的利润最大.