题目内容
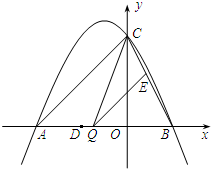
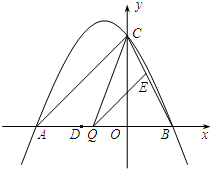
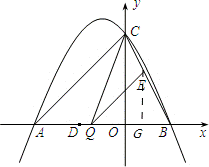
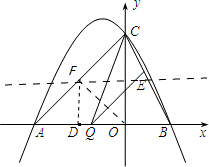
(2011•广元)如图,抛物线y=ax2+2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A(﹣4,0)和B.(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CEQ的面积最大时,求点Q的坐标;
(3)平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(﹣2,0).问是否有直线l,使△ODF是等腰三角形?若存在,请求出点F的坐标;若不存在,请说明理由.
解:(1)由题意,得: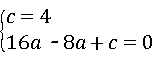 ,
,
解得: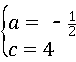 ,
,
∴所求抛物线的解析式为:y=﹣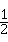 x2﹣x+4.
x2﹣x+4.
(2)设点Q的坐标为(m,0),过点E作EG⊥x轴于点G.
由﹣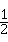 x2﹣x+4=0,
x2﹣x+4=0,
得x1=2,x2=﹣4,
∴点B的坐标为(2,0),
∴AB=6,BQ=2﹣m,
∵QE∥AC,
∴△BQE∽△BAC,
∴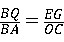 ,
,
即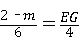 ,
,
∴EG=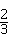 (2﹣m),
(2﹣m),
∴S△CQE=S△CBQ﹣S△EBQ
=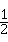 BQ•CO﹣
BQ•CO﹣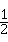 BQ•EG
BQ•EG
=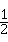 (2﹣m)[4﹣
(2﹣m)[4﹣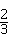 (2﹣m)]
(2﹣m)]
=﹣(m+1)2+3
又∵﹣4≤m≤2,
∴当m=﹣1时,S△CQE有最大值3,此时Q(﹣1,0).
(3)存在.在△ODF中.
(ⅰ)若DO=DF,
∵A(﹣4,0),D(﹣2,0)
∴AD=OD=DF=2,
又在Rt△AOC中,OA=OC=4,
∴∠OAC=45°,
∴∠DFA=∠OAC=45°,
∴∠ADF=90°.
此时,点F的坐标为(﹣2,2)
由﹣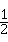 x2﹣x+4=2,
x2﹣x+4=2,
得x1=﹣1+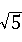 ,x2=﹣1﹣
,x2=﹣1﹣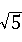 ,
,
此时,点P的坐标为:P(﹣1+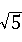 ,2)或P(﹣1﹣
,2)或P(﹣1﹣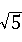 ,2).
,2).
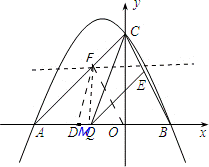
(ⅱ)若FO=FD,过点F作FM⊥x轴于点M
由等腰三角形的性质得:OM=OD=1,
∴AM=3,
∴在等腰直角△AMF中,MF=AM=3,
∴F(﹣1,3)
由﹣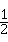 x2﹣x+4=3,
x2﹣x+4=3,
得x1=﹣1+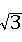 ,x2=﹣1﹣
,x2=﹣1﹣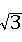 ,
,
此时,点P的坐标为:P(﹣1+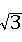 ,3)或P(﹣1﹣
,3)或P(﹣1﹣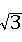 ,3).
,3).
(ⅲ)若OD=OF,
∵OA=OC=4,且∠AOC=90°,
∴AC=4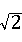 ,
,
∴点O到AC的距离为2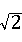 ,而OF=OD=2<2
,而OF=OD=2<2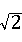 ,
,
∴此时不存在这样的直线l,使得△ODF是等腰三角形,
综上所述,存在这样的直线l,使得△ODF是等腰三角形,
所求点P的坐标为:P(﹣1+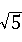 ,2)或P(﹣1﹣
,2)或P(﹣1﹣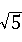 ,2)或P(﹣1+
,2)或P(﹣1+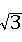 ,3)或P(﹣1﹣
,3)或P(﹣1﹣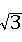 ,3).解析:
,3).解析:
略
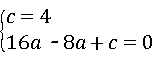 ,
,解得:
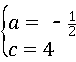 ,
,∴所求抛物线的解析式为:y=﹣
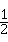 x2﹣x+4.
x2﹣x+4.(2)设点Q的坐标为(m,0),过点E作EG⊥x轴于点G.

由﹣
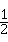 x2﹣x+4=0,
x2﹣x+4=0,得x1=2,x2=﹣4,
∴点B的坐标为(2,0),
∴AB=6,BQ=2﹣m,
∵QE∥AC,
∴△BQE∽△BAC,
∴
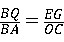 ,
,即
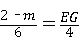 ,
,∴EG=
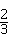 (2﹣m),
(2﹣m),∴S△CQE=S△CBQ﹣S△EBQ
=
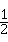 BQ•CO﹣
BQ•CO﹣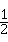 BQ•EG
BQ•EG=
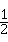 (2﹣m)[4﹣
(2﹣m)[4﹣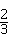 (2﹣m)]
(2﹣m)]=﹣(m+1)2+3
又∵﹣4≤m≤2,
∴当m=﹣1时,S△CQE有最大值3,此时Q(﹣1,0).
(3)存在.在△ODF中.

(ⅰ)若DO=DF,
∵A(﹣4,0),D(﹣2,0)
∴AD=OD=DF=2,
又在Rt△AOC中,OA=OC=4,
∴∠OAC=45°,
∴∠DFA=∠OAC=45°,
∴∠ADF=90°.
此时,点F的坐标为(﹣2,2)
由﹣
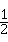 x2﹣x+4=2,
x2﹣x+4=2,得x1=﹣1+
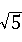 ,x2=﹣1﹣
,x2=﹣1﹣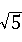 ,
,此时,点P的坐标为:P(﹣1+
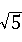 ,2)或P(﹣1﹣
,2)或P(﹣1﹣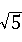 ,2).
,2).
(ⅱ)若FO=FD,过点F作FM⊥x轴于点M
由等腰三角形的性质得:OM=OD=1,
∴AM=3,
∴在等腰直角△AMF中,MF=AM=3,
∴F(﹣1,3)
由﹣
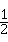 x2﹣x+4=3,
x2﹣x+4=3,得x1=﹣1+
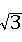 ,x2=﹣1﹣
,x2=﹣1﹣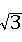 ,
,此时,点P的坐标为:P(﹣1+
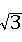 ,3)或P(﹣1﹣
,3)或P(﹣1﹣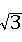 ,3).
,3).(ⅲ)若OD=OF,
∵OA=OC=4,且∠AOC=90°,
∴AC=4
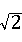 ,
,∴点O到AC的距离为2
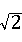 ,而OF=OD=2<2
,而OF=OD=2<2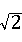 ,
,∴此时不存在这样的直线l,使得△ODF是等腰三角形,
综上所述,存在这样的直线l,使得△ODF是等腰三角形,
所求点P的坐标为:P(﹣1+
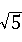 ,2)或P(﹣1﹣
,2)或P(﹣1﹣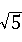 ,2)或P(﹣1+
,2)或P(﹣1+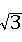 ,3)或P(﹣1﹣
,3)或P(﹣1﹣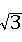 ,3).解析:
,3).解析:略

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
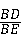 =
=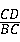 ;
;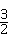 AB,求tan∠CDF的值.
AB,求tan∠CDF的值.