题目内容
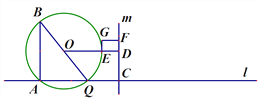
【题目】如图，点A在直线l上，点Q沿着直线l以3厘米／秒的速度由点A向右运动，以AQ为边作Rt
，使∠BAQ=90°，
，点C在点Q右侧，CQ=1厘米，过点C作直线m⊥l，过
的外接圆圆心O作OD⊥m于点D，交AB右侧的圆弧于点E．在射线CD上取点F，使DF=
CD，以DE、DF为邻边作矩形DEGF．设运动时间为t秒.
(1)直接用含t的代数式表示BQ、DF；
(2)当0＜t＜1时，求矩形DEGF的最大面积；
(3)点Q在整个运动过程中，当矩形DEGF为正方形时，求t的值.
【答案】（1）
， 
；
（2）矩形DEGF的最大面积为
；
（3）
或
【解析】试题分析：（1）AB与OD交于点H ，根据题中的比例关系和勾股定理可表示出BQ的长；根据垂直于同一条直线的两直线平行和三角形的中位线定理可求得AH的长，再根据矩形的判定定理和矩形的性质可求CD的长，即可表示出FD；
（2）根据题意表示出矩形的长和宽，然后构造二次函数，通过二次函数的最值可求解；
（3）当矩形为正方形时，分别让其长与宽相等，列方程求解即可.
试题解析：（1）
， 
；
（2）DE=OD-OE=
t+1-
t=1-t， 
，∴当t=
时，矩形DEGF的最大面积为
；
（3）当矩形DEGF为正方形时， 
,解得
.
练习册系列答案
相关题目
