题目内容
【题目】当我们利用2种不同的方法计算同一图形的面积时，可以得到一个等式．例如，由图1可得等式：（a+2b）（a+b）=a2+3ab+2b2．
（1）由图2，可得等式：_____________________________
（2）利用（1）中所得到的结论，解决下面的问题：
已知 a+b+c=11，ab+bc+ac=38，求a2+b2+c2的值；
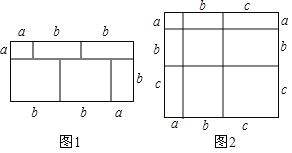
【答案】（1）等式为（a+b+c）2=a2+b2+c2+2ab+2ac+2bc．（2）45.
【解析】试题分析：（1）根据图2，利用直接求与间接法分别表示出正方形面积，即可确定出所求等式；
（2）根据（1）中结果，求出所求式子的值即可.
试题解析：（1）（a+b+c）2=a2+b2+c2+2ab+2ac+2bc；
（2）∵a+b+c=11，ab+bc+ac=38，
∴a2+b2+c2=（a+b+c）2-2（ab+ac+bc）=121-76=45.
练习册系列答案
相关题目
