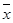题目内容
某射击队要从五名队员中选拔一名运动员参加比赛,选拔赛中每名队员的平均数与方差如表所示,如果要选择一个成绩高且发挥又稳定的人参赛,则应选( )
| 甲 | 乙 | 丙 | 丁 | 戊 | |||
|
8.5 | 9.0 | 9.0 | 8.5 | 8.5 | ||
| S2 | 0.9 | 1.3 | 0.9 | 1.0 | 1.2 |
| A、甲 | B、乙 | C、丙 | D、丁 |
分析:看图:选择平均数大,方差小的人参赛即可.
解答:解:观察图形可知甲、丙方差相等,但都小于乙、丁、戊,
∴只要比较甲、丙就可得出正确结果,
∵甲的平均数小于丙的平均数,
∴丙的成绩高且发挥稳定.
故选C.
∴只要比较甲、丙就可得出正确结果,
∵甲的平均数小于丙的平均数,
∴丙的成绩高且发挥稳定.
故选C.
点评:本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
某射击队要从五名队员中选拔一名运动员参加比赛,选拔赛中每名队员的平均数与方差如表所示,如果要选择一个成绩高且发挥又稳定的人参赛,则应选( )
A.甲 B.乙 C.丙 D.丁
|
|
甲 |
乙 |
丙 |
丁 |
戊 |
|
|
8.5 |
9.0 |
9.0 |
8.5 |
8.5 |
|
S2 |
0.9 |
1.3 |
0.9 |
1.0 |
1.2 |
某射击队要从五名队员中选拔一名运动员参加比赛,选拔赛中每名队员的平均数与![]() 方差如表所示,如果要选择一个成绩高且发挥又稳定的人参赛,则应选( )
方差如表所示,如果要选择一个成绩高且发挥又稳定的人参赛,则应选( )
A.甲 B.乙 C.丙 D.丁
| 甲 | 乙 | 丙 | 丁 | 戊 | |
|
| 8.5 | 9.0 | 9.0 | 8.5 | 8.5 |
| S2 | 0.9 | 1.3 | 0.9 | 1.0 | 1.2 |
某射击队要从五名队员中选拔一名运动员参加比赛,选拔赛中每名队员的平均数与方差如表所示,如果要选择一个成绩高且发挥又稳定的人参赛,则应选( )
| A.甲 | B.乙 | C.丙 | D.丁 |
| | 甲 | 乙 | 丙 | 丁 | 戊 |
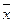 | 8.5 | 9.0 | 9.0 | 8.5 | 8.5 |
| S2 | 0.9 | 1.3 | 0.9 | 1.0 | 1.2 |
某射击队要从五名队员中选拔一名运动员参加比赛,选拔赛中每名队员的平均数与方差如表所示,如果要选择一个成绩高且发挥又稳定的人参赛,则应选( )
| A.甲 | B.乙 | C.丙 | D.丁 |
| | 甲 | 乙 | 丙 | 丁 | 戊 |
 | 8.5 | 9.0 | 9.0 | 8.5 | 8.5 |
| S2 | 0.9 | 1.3 | 0.9 | 1.0 | 1.2 |