题目内容
(2012•广元)已知关于x的方程(x+1)2+(x-b)2=2有唯一的实数解,且反比例函数y=
的图象在每个象限内y随x的增大而增大,那么反比例函数的关系式为( )
| 1+b |
| x |
分析:关于x的方程(x+1)2+(x-b)2=2有唯一的实数解,则判别式等于0,据此即可求得b的值,然后根据反比例函数y=
的图象在每个象限内y随x的增大而增大,则比例系数1+b<0,则b的值可以确定,从而确定函数的解析式.
| 1+b |
| x |
解答:解:关于x的方程(x+1)2+(x-b)2=2化成一般形式是:2x2+(2-2b)x+(b2-1)=0,
△=(2-2b)2-8(b2-1)=-4(b+3)(b-1)=0,
解得:b=-3或1.
∵反比例函数y=
的图象在每个象限内y随x的增大而增大,
∴1+b<0
∴b<-1,
∴b=-3.
则反比例函数的解析式是:y=
,即y=-
.
故选D.
△=(2-2b)2-8(b2-1)=-4(b+3)(b-1)=0,
解得:b=-3或1.
∵反比例函数y=
| 1+b |
| x |
∴1+b<0
∴b<-1,
∴b=-3.
则反比例函数的解析式是:y=
|
| 2 |
| x |
故选D.
点评:本题考查了反比例函数的性质,以及一元二次方程的根的判别式,正确利用判别式求得b的值是关键.

练习册系列答案
相关题目
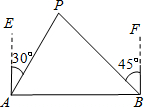 (2012•广元)如图,A、B两座城市相距100千米,现计划要在两座城市之间修筑一条高等级公路(即线段AB).经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上.已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内.请问:计划修筑的这条高等级公路会不会穿越森林保护区?为什么?
(2012•广元)如图,A、B两座城市相距100千米,现计划要在两座城市之间修筑一条高等级公路(即线段AB).经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上.已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内.请问:计划修筑的这条高等级公路会不会穿越森林保护区?为什么?