题目内容
15.已知直角三角形两直角边分别为9、12,则斜边上的高为$\frac{36}{5}$.分析 根据勾股定理可求出斜边.然后由于同一三角形面积一定,即可得出结果.
解答 解:∵直角三角形的两条直角边分别为9、12,
∴斜边长=$\sqrt{{9}^{2}+1{2}^{2}}$=15,
设斜边上的高为h,
则直角三角形的面积为$\frac{1}{2}$×9×12=$\frac{1}{2}$×15•h,
∴h=$\frac{9×12}{15}$=$\frac{36}{5}$;
故答案为:$\frac{36}{5}$.
点评 本题考查了勾股定理的运用、直角三角形的面积的求法,熟练掌握勾股定理是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.方程ax+5=11的解是x=2,则a的值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
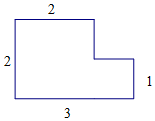 有一块木板,如图,请你把它切成三块,然后拼成一个正方形的桌面.请在图中画出剪切线,并把拼成的正方形在图中画出(保留剪切的痕迹,不写画法)
有一块木板,如图,请你把它切成三块,然后拼成一个正方形的桌面.请在图中画出剪切线,并把拼成的正方形在图中画出(保留剪切的痕迹,不写画法)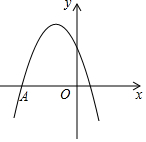 如图是二次函数y=ax2+bx+c图象的一部分,图象经过点A(-3,0)对称轴为直线x=-1,给出以下5个结论:①abc>0;②b2>4ac;③2a+b=0;④a+bc>0;⑤若点B(-$\frac{5}{2}$,y1),C(-$\frac{1}{2}$,y2)为函数图象上的两点,则y1<y2.其中正确的序号为①②⑤.
如图是二次函数y=ax2+bx+c图象的一部分,图象经过点A(-3,0)对称轴为直线x=-1,给出以下5个结论:①abc>0;②b2>4ac;③2a+b=0;④a+bc>0;⑤若点B(-$\frac{5}{2}$,y1),C(-$\frac{1}{2}$,y2)为函数图象上的两点,则y1<y2.其中正确的序号为①②⑤.