题目内容
如图，已知在⊙O中，直径MN=10，正方形ABCD的四个顶点分别在⊙O及半径OM、OP上，并且∠POM=45°，则AB的长为 ．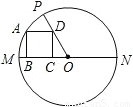
【答案】分析：首先得出△CDO为等腰直角三角形，可知CO=CD，在直角三角形OAB中依据勾股定理即可解决．
解答：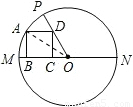
解：∵∠POM=45°，∠DCO=90°，
∴∠DOC=∠CDO=45°，
∴△CDO为等腰直角三角形，
那么CO=CD．
连接OA，可得到直角三角形OAB，
∴AB=BC=CD=CO，BO=BC+CO=BC+CD=2AB，
那么AB2+OB2=52，
∴AB2+（2AB）2=52，
∴AB的长为
．
点评：解决本题的关键是构造直角三角形，注意先得到OB=2AB．
解答：
解：∵∠POM=45°，∠DCO=90°，∴∠DOC=∠CDO=45°，
∴△CDO为等腰直角三角形，
那么CO=CD．
连接OA，可得到直角三角形OAB，
∴AB=BC=CD=CO，BO=BC+CO=BC+CD=2AB，
那么AB2+OB2=52，
∴AB2+（2AB）2=52，
∴AB的长为
．点评：解决本题的关键是构造直角三角形，注意先得到OB=2AB．
练习册系列答案
相关题目
20、如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F．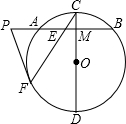
作⊙O的切线交BA的延长线于点P．
（2011•普宁市一模）如图，已知在?ABCD中，E、F是对角线BD延长线上的两点，且∠BCE=∠DAF，求证：△ECD≌△FAB．
如图，已知在△ABC中，AB=AC，AB的垂直平分线DE交AC于点E，CE的垂直平分线正好经过点B，与AC相交于点F，求∠A的度数．