Question

【题目】如图，Rt△ABC中，∠C=90°，∠A=30°，BC=6．

（1）实践操作：尺规作图，不写作法，保留作图痕迹．

①作∠ABC的角平分线交AC于点D．

②作线段BD的垂直平分线，交AB于点E，交BC于点F，连接DE、DF．

（2）推理计算：四边形BFDE的面积为　 　．

Answer 1

【答案】(1)详见解析;(2).

【解析】

（1）利用基本作图（作一个角等于已知角和作已知线段的垂直平分线）作出BD和EF；

（2）先证明四边形BEDF为菱形，再利用含30度的直角三角形三边的关系求出BF和CD，然后利用菱形的面积公式求解．

（1）如图，DE、DF为所作；

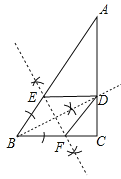
（2）∵∠C=90°，∠A=30°，∴∠ABC=60°，AB=2BC=12．

∵BD为∠ABC的角平分线，∴∠DBC=∠EBD=30°．

∵EF垂直平分BD，∴FB=FD，EB=ED，∴∠FDB=∠DBC=30°，∠EDB=∠EBD=30°，∴DE∥BF，BE∥DF，∴四边形BEDF为平行四边形，而FB=FD，∴四边形BEDF为菱形．

∵∠DFC=∠FBD+∠FDB=30°+30°=60°，∴∠FDC=90°－60°=30°．在Rt△BDC中，∵BC=6，∠DBC=30°，∴DC=．在Rt△FCD中，∵∠FDC=30°，∴FC=2，∴FD=2FC=4，∴BF=FD=4，∴四边形BFDE的面积=4×2=8．

故答案为：8．