题目内容
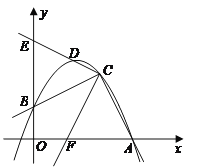
【题目】如图,已知二次函数![]() 的图象经过A(3,0),B(0,1),C(2,2)三点.
的图象经过A(3,0),B(0,1),C(2,2)三点.
(1)求二次函数![]() 的解析式;
的解析式;
(2)设点D(![]() ,m )在二次函数的图象上,将∠ACB绕点C按顺时针方向旋转至∠FCE,使得射线CE与
,m )在二次函数的图象上,将∠ACB绕点C按顺时针方向旋转至∠FCE,使得射线CE与![]() 轴的正半轴交于点E,且经过点D,射线CF与线段OA交于点F.求证:BE=2FO;
轴的正半轴交于点E,且经过点D,射线CF与线段OA交于点F.求证:BE=2FO;
(3)是否存在点H(n,2),使得点A、D、H构成的△ADH是直角三角形?若存在,有几个符合条件的点H?(直接回答,不必说明理由)
【答案】(1)二次函数的解析式为![]() ;
;
(2)证明见解析;
(3)存在4个符合条件的点H,使得点A、D、H构成的△ADH是直角三角形.
【解析】(1)用待定系数法求出抛物线解析式即可;(2)证明Rt△NBC≌Rt△MAC和△ACF≌△BCE, 得出AF=BE,然后利用一次函数求出BE=2FO;(3)最后直接求出符合条件△ADH是直角三角形的点H.
(1)解:把A(3,0),B(0,1),C(2,2)代入![]() ,
,
得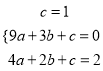 ∴
∴

∴二次函数的解析式为![]() .
.
(2)过点C作CM⊥OA于点M,CN⊥y轴于点N,

∵A(3,0),B(0,1),C(2,2),
∴CM= CN=2,CA=CB=![]() ,
, ![]()
∴Rt△NBC≌Rt△MAC,
∴∠CAF=∠CBE,
∵将∠ACB绕点C按顺时针方向旋转至∠FCE,
∴∠FCE=∠ACB,
∴∠FCE-∠BCF=∠ACB-∠BCF,
即∠ACF=∠BCE,
又∵CB=CA,∴△ACF≌△BCE,
∴AF=BE.
∵二次函数的解析式为![]() ,
,
当![]() 时,
时, ![]() ,∴
,∴![]()
设直线CD: ![]() ,把C(2,2)、
,把C(2,2)、![]() 代入得
代入得
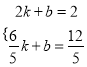 , 解得
, 解得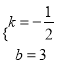 ,
,
∴直线CD: ![]() .
.
∴E(0,3),BE=2, ∴AF=BE=2 ,
∴FO=OA-AF=1.
∴BE=2FO.
(3)存在4个符合条件的点H,使得点A、D、H构成的△ADH是直角三角形.
“点睛”本题考查了二次函数的综合题,熟练掌握运用待定系数法求函数解析式;熟练掌握二次函数图象上点的坐标特征,根据题意利用一次函数求出BE=2FO是解答此题的关键.
