Question

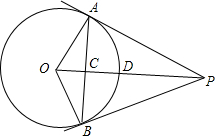如图，P是⊙O外一点，OP垂直于弦AB于点C，交

AB

于点D，连接OA、OB、AP、BP．根据以上条件，写出三个正确结论（OA=OB除外）：①

 

；②

 

；③

 

．

Answer 1

分析：根据垂径定理写出相关的结论即可．

解答：解：如：①∠OAB=∠OBA．
证明：因为OA=OB=r
∴△OAB为等腰三角形
∴∠OAB=∠OBA；
②AC=BC．
证明：∵OA=OB
∠OAP=∠OBP=90°
OP=OP
∴根据HL定理，△OAP≌△OBP
∴∠AOP=∠BOP
又∵△OAB为等腰三角形
∴AC=BC；
③△OAC≌△OBC．
证明：∵OA=OB
∠AOC=∠BOC
OC=OC
∴△OAC≌△OBC．

点评：本题主要考查了垂径定理的应用，学生一定要学以致用．答案不唯一，只要能根据垂径定理得出结论即可．