题目内容
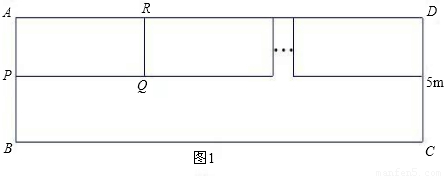
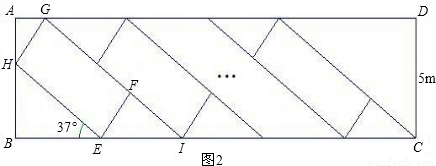
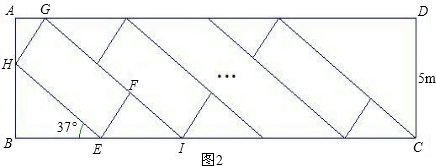
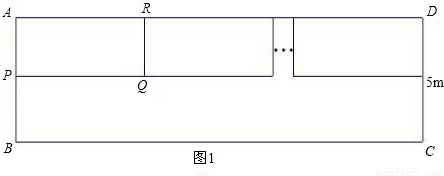
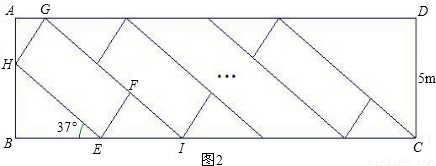
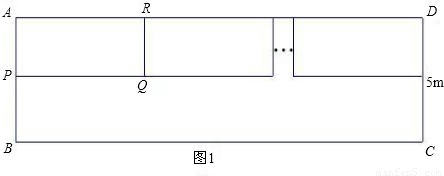
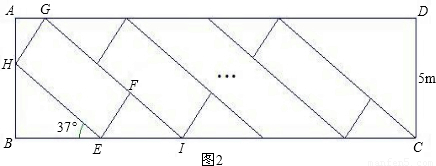
小明家新买了一辆小汽车,可是小区内矩形停车场ABCD只有9个已停满车的车位(图1中的小矩形APQR等),该矩形停车场的可用宽度(CD)只有5米.由于种种原因,车位不能与停车场的长边BC垂直设计.为了增加车位,小明设计出了图2的停车方案,每个车位(图2中的小矩形EFGH等)与该停车场的长边的夹角为37°,且每个车位的宽与原来车位保持不变,每个车位的长比原来车位少1米.这样,总共比原来多了3个车位、设现在每个车位的长为x米,宽为y米,(参考数据:sin37°=
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 4 |
(1)请用含x的代数式表示BE;用含y的代数式表示AH;
(2)求现在每个车位的长和宽各是多少米?
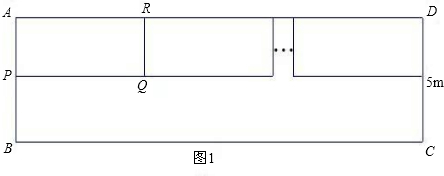

分析:(1)易得∠AHG=37°,利用37°的余弦值即可求得AH;利用37°的余弦值即可求得BE的长;
(2)易得∠EIF=37°,利用37°的正弦值可求得EI的长度,根据AH与BH的和为5m,BE长+(9+3)EI=9×原来的车长.
(2)易得∠EIF=37°,利用37°的正弦值可求得EI的长度,根据AH与BH的和为5m,BE长+(9+3)EI=9×原来的车长.
解答:解:
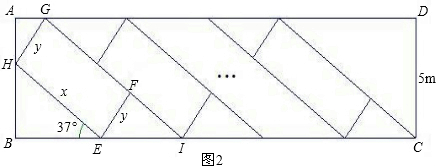
(1)∵∠GHE=∠B=90°,
∴∠AHG+∠BHE=90°,∠BEH+∠BHE=90°,
∴∠AHG=∠BEH=37°,
∴在Rt△AHG中,AH=HG•cos∠AHG=y•cos37°=
y(1分),
在Rt△BHE中,BH=HE•sin∠BEH=x•sin37°=
x,
BE=HE•cos∠BEH=x•cos37°=
x;(2分)
(2)在Rt△EFI中,∠EIF=37°,
∴EI=
=
=
y(3分),
根据题意,得
(6分),
解得
(7分),
答:现在每个车位的长为5m,宽为2.5m.(8分)

(1)∵∠GHE=∠B=90°,
∴∠AHG+∠BHE=90°,∠BEH+∠BHE=90°,
∴∠AHG=∠BEH=37°,
∴在Rt△AHG中,AH=HG•cos∠AHG=y•cos37°=
| 4 |
| 5 |
在Rt△BHE中,BH=HE•sin∠BEH=x•sin37°=
| 3 |
| 5 |
BE=HE•cos∠BEH=x•cos37°=
| 4 |
| 5 |
(2)在Rt△EFI中,∠EIF=37°,
∴EI=
| EF |
| sin∠EIF |
| y |
| sin37° |
| 5 |
| 3 |
根据题意,得
|
解得
|
答:现在每个车位的长为5m,宽为2.5m.(8分)
点评:考查锐角三角函数的应用,关键是根据停车场的长与宽得到相应的等量关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,cos37°=
,cos37°= ,tan37°=
,tan37°= )
)
 ,cos37°=
,cos37°= ,tan37°=
,tan37°= )
)
 ,cos37°=
,cos37°= ,tan37°=
,tan37°= )
)
 ,cos37°=
,cos37°= ,tan37°=
,tan37°= )
)