题目内容
如果顺次连接一个四边形四边中点所得的四边形是菱形,则该四边形的两条对角线必须满足( )
分析:根据三角形中位线的性质得到EH=
AC,EH∥AC,FG=
AC,FG∥AC,可得四边形EFGH为平行四边形,要得到四边形EFGH为菱形,则EH=EF,而EF=
BD,所以当AC=BD时可得到四边形EFGH为菱形.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:如图,连接AC,BD.点E、F、G、H分别为四边形ABCD各边中点,
解:如图,连接AC,BD.点E、F、G、H分别为四边形ABCD各边中点,
∴EH=
AC,EH∥AC,FG=
AC,FG∥AC,
∴四边形EFGH为平行四边形,
当EH=EF时,四边形EFGH为菱形,
又∵EF=
BD,
若EH=EF,
则AC=BD.即该四边形的两条对角线相等.
故选C.
 解:如图,连接AC,BD.点E、F、G、H分别为四边形ABCD各边中点,
解:如图,连接AC,BD.点E、F、G、H分别为四边形ABCD各边中点,∴EH=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形EFGH为平行四边形,
当EH=EF时,四边形EFGH为菱形,
又∵EF=
| 1 |
| 2 |
若EH=EF,
则AC=BD.即该四边形的两条对角线相等.
故选C.
点评:本题考查了菱形的判定定理:邻边相等的平行四边形是菱形.也考查了平行四边形的判定以及三角形中位线的性质.

练习册系列答案
相关题目
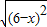 =x-6成立的条件是x<6
=x-6成立的条件是x<6