题目内容
增根是在分式方程转化为整式方程的过程中产生的,分式方程的增根,不是分式方程的根,而是该分式方程化成的整式方程的根,所以涉及分式方程的增根问题的解题步骤通常为:①去分母,化分式方程为整式方程;②将增根代入整式方程中,求出方程中字母系数的值.阅读以上材料后,完成下列探究:
探究1:m为何值时,方程
| 3x |
| x-3 |
| m |
| 3-x |
探究2:m为何值时,方程
| 3x |
| x-3 |
| m |
| 3-x |
探究3:任意写出三个m的值,使对应的方程
| 3x |
| x-3 |
| m |
| 3-x |
探究4:你发现满足“探究3”条件的m1、m2、m3的关系是
分析:解分式方程,根据方程有增根求得m的值即可,根据规律即可得出结论.第三问设方程的三根为a,b,c且a+b=c,再求得对应的m.即可得出它们之间的关系.
解答:解:探究1:方程两边都乘(x-3),
得3x+5(x-3)=-m
∵原方程有增根,
∴最简公分母(x-3)=0,
解得x=3,
当x=3时,m=-9,
故m的值是-9.
探究2:方程两边都乘(x-3),
得3x+5(x-3)=-m
∵原方程的根为x=-1,
∴m=23,
探究3:由(1)(2)得x=
,
方程的三个对应根为a,b,c且a+b=c,
即可得出对应的m,m1=15-8a,m2=15-8b,m3=15-8c,
探究4:∵a+b=c,
∴
+
=
,
整理得m3=m1+m2-15,
故答案为m3=m1+m2-15.
得3x+5(x-3)=-m
∵原方程有增根,
∴最简公分母(x-3)=0,
解得x=3,
当x=3时,m=-9,
故m的值是-9.
探究2:方程两边都乘(x-3),
得3x+5(x-3)=-m
∵原方程的根为x=-1,
∴m=23,
探究3:由(1)(2)得x=
| 15-m |
| 8 |
方程的三个对应根为a,b,c且a+b=c,
即可得出对应的m,m1=15-8a,m2=15-8b,m3=15-8c,
探究4:∵a+b=c,
∴
| 15-m1 |
| 8 |
| 15-m2 |
| 8 |
| 15-m3 |
| 8 |
整理得m3=m1+m2-15,
故答案为m3=m1+m2-15.
点评:本题考查了分式方程的增根,解分式方程要验根,但解含有字母参数的分式方程不用验根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
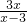 +5=
+5= 有增根.
有增根.