��Ŀ����
Ӧ�ù��ɣ��������
��1�������壺aΪ������1�������������ǰ�
��Ϊa�IJ�����磺2�IJ����
=
=-1��-1�IJ����
=
����֪a1=-
��
��a2��a1�IJ������a2=
��
��a3��a2�IJ������a3=
��a4��a3�IJ������a4=
���Դ����ƣ�a2011=
��2��������֪����
��
=
��
��
��
=
������
��
��
������
=
���Ը���������ɣ�
���㣺(
-1)(
-1)(
-1)��(
-1)��
��1�������壺aΪ������1�������������ǰ�
| 1 |
| 1-a |
| 1 |
| 1-2 |
| 1 |
| -1 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |
| 1 |
| 3 |
��a2��a1�IJ������a2=
| 3 |
| 4 |
| 3 |
| 4 |
��a3��a2�IJ������a3=
4
4
����a4��a3�IJ������a4=
-
| 1 |
| 3 |
-
��| 1 |
| 3 |
���Դ����ƣ�a2011=
-
| 1 |
| 3 |
-
��| 1 |
| 3 |
��2��������֪����
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| n |
| n+1 |
| 1 |
| n+1 |
���㣺(
| 1 |
| 19 |
| 1 |
| 20 |
| 1 |
| 21 |
| 1 |
| 2011 |
��������1���������ĸ��Ҫ���ݶ���ȥ����ͨ�����㣬Ѱ�Ҳ�����ֵĹ��ɣ����ݹ��ɽ�ɣ�
��2������
��
=
��
��
��
=
������
��
��
������
=
���ɵó��𰸼��ɣ�
��2������
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| n |
| n+1 |
| 1 |
| n+1 |
����⣺��1�����ݲ������ɵã���a2=
=
=
��
��a3=
=
=4��
��a4=
=
=-
��
����Ȼÿ����ѭ��һ�Σ���2011��3=670��1����a2011��a1��ֵ��ȣ�
��a2011=-
��
��2��(
-1)(
-1)(
-1)��(
-1)��
=-
����-
������-
������-
����
=-
��
�ʴ�Ϊ����
��4����-
����
��
| 1 |
| 1-a1 |
| 1 | ||
1+
|
| 3 |
| 4 |
��a3=
| 1 |
| 1-a2 |
| 1 | ||
1-
|
��a4=
| 1 |
| 1-a3 |
| 1 |
| 1-4 |
| 1 |
| 3 |
����Ȼÿ����ѭ��һ�Σ���2011��3=670��1����a2011��a1��ֵ��ȣ�
��a2011=-
| 1 |
| 3 |
��2��(
| 1 |
| 19 |
| 1 |
| 20 |
| 1 |
| 21 |
| 1 |
| 2011 |
=-
| 18 |
| 19 |
| 19 |
| 20 |
| 20 |
| 21 |
| 2010 |
| 2011 |
=-
| 18 |
| 2011 |
�ʴ�Ϊ����
| 3 |
| 4 |
| 1 |
| 3 |
| 3 |
| 4 |
������������Ҫ���������ֹ��ɣ���������Ҫ�ϸ���ݶ���������Ҳ�ǽ�������ֵ���������֮һ��ͬʱע�����ѭ���Ĺ��ɣ�

��ϰ��ϵ�д�
 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�
�����Ŀ
 ���������֡�
���������֡�
 ����ͼ��1����ֱ��l����2���㣬��1���߶Σ�
����ͼ��1����ֱ��l����2���㣬��1���߶Σ�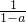 ��Ϊa�IJ�����磺2�IJ����
��Ϊa�IJ�����磺2�IJ����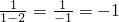 ��-1�IJ����
��-1�IJ����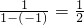 ����֪
����֪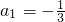 ��
��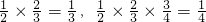 ������
������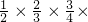 ����
����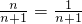 ���Ը���������ɣ�
���Ը���������ɣ�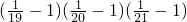 ��
��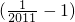 ��
��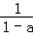 ��Ϊa�IJ�����磺2�IJ����
��Ϊa�IJ�����磺2�IJ����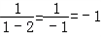 ����1�IJ����
����1�IJ����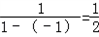 ����֪
����֪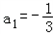 ��
��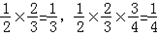 ������
������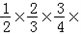 ����
����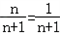 ���Ը���������ɣ����㣺
���Ը���������ɣ����㣺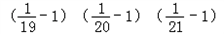 ��
��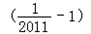 ��
��