题目内容
正方形OABC的边长为2,把它放在如图所示的直角坐标系中,点M(t,0)是X轴上一个动点,连接BM,在BM的右侧作正方形BMNP;直线DE的解析式为y=2x+b,与X轴交于点D,与Y轴交于点E,当三角形PDE为等腰直角三角形时,点P的坐标是 .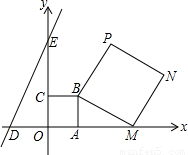
【答案】分析:过点P作PF⊥BC交CB的延长线于点F,根据同角的余角相等可得∠ABM=∠FBP,然后利用“角角边”证明△ABM和△FBP全等,根据全等三角形对应边相等可得BF=AB,PF=AM,然后根据正方形OABC的边长为2以及点M(t,0)表示出点P的坐标,再利用直线DE的解析式求出点D、E的坐标,然后分①DE是斜边时,利用勾股定理以及两点间的距离公式分别表示出PD、PE、DE的平方,再根据等腰直角三角形的三边关系,②PD是斜边时,过点P作PF⊥y轴于点F,然后利用“角角边”证明△EDO和△PEF全等,根据全等三角形对应边相等可得EF=DO,PC=EO,然后用b、t表示并求解即可得到点P的坐标.
解答:解:如图,过点P作PF⊥BC交CB的延长线于点F,
∵四边形OABC与四边形BMNP都是正方形,
∴∠ABM+∠MBF=90°,
∠FBP+∠MBF=90°,
∴∠ABM=∠FBP,
在△ABM和△FBP中,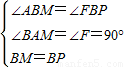 ,
,
∴△ABM≌△FBP(AAS),
∴BF=AB,PF=AM,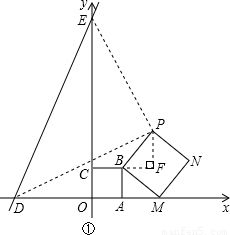
∵正方形OABC的边长为2,点M(t,0),
∴BF=2,PF=t-2,
点P到x轴的距离为t-2+2=t,
∴点P的坐标为(4,t),
又∵当y=0时,2x+b=0,解得x=-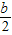 ,
,
当x=0时,y=b,
∴点D(-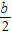 ,0),E(0,b),
,0),E(0,b),
①DE是斜边时,
PD2=(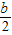 +4)2+t2,PE2=(b-t)2+42,DE2=(
+4)2+t2,PE2=(b-t)2+42,DE2=(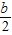 )2+b2,
)2+b2,
∵△PDE是等腰直角三角形,
∴PD2=PE2,且PD2+PE2=DE2,
即(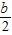 +4)2+t2=(b-t)2+42,且(
+4)2+t2=(b-t)2+42,且(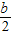 +4)2+t2+(b-t)2+42=(
+4)2+t2+(b-t)2+42=(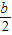 )2+b2,
)2+b2,
 b2+4b+16+t2=b2-2bt+t2+16,且
b2+4b+16+t2=b2-2bt+t2+16,且 b2+4b+16+t2+b2-2bt+t2+16=
b2+4b+16+t2+b2-2bt+t2+16= b2+b2,
b2+b2,
整理得,b= (t+2)且t2-b(t-2)+16=0,
(t+2)且t2-b(t-2)+16=0,
∴t2- (t+2)(t-2)+16=0,
(t+2)(t-2)+16=0,
整理得,t2=16,
解得t1=4,t2=-4(舍去),
∴点P的坐标是(4,4);
②PD是斜边时,∵△PDE是等腰直角三角形,
∴PE⊥DE,且PE=DE,
过点P作PF⊥y轴于点F,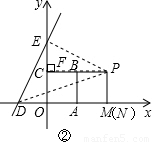
∵∠DEO+∠PEO=90°,∠DEO+∠EDO=90°,
∴∠PEO=∠EDO,
在△EDO和△PEF中,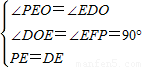 ,
,
∴△EDO≌△PEF(AAS),
∴EF=DO=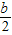 ,PC=EO=b,
,PC=EO=b,
又∵点P(4,t),
∴b=4,b-t=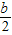 ,
,
解得t=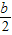 =
= ×4=2,
×4=2,
∴点P坐标为(4,2),
此时点C、F重合,点M、N重合,
综上所述,点P的坐标为(4,4)或(4,2).
故答案为:(4,4)或(4,2).
点评:本题是一次函数的综合题型,主要利用了全等三角形的判定与性质,等腰三角形的性质,直线与坐标轴的交点的求解,勾股定理的应用,综合题但难度不大,要注意分情况讨论.
解答:解:如图,过点P作PF⊥BC交CB的延长线于点F,
∵四边形OABC与四边形BMNP都是正方形,
∴∠ABM+∠MBF=90°,
∠FBP+∠MBF=90°,
∴∠ABM=∠FBP,
在△ABM和△FBP中,
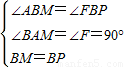 ,
,∴△ABM≌△FBP(AAS),
∴BF=AB,PF=AM,

∵正方形OABC的边长为2,点M(t,0),
∴BF=2,PF=t-2,
点P到x轴的距离为t-2+2=t,
∴点P的坐标为(4,t),
又∵当y=0时,2x+b=0,解得x=-
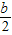 ,
,当x=0时,y=b,
∴点D(-
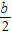 ,0),E(0,b),
,0),E(0,b),①DE是斜边时,
PD2=(
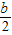 +4)2+t2,PE2=(b-t)2+42,DE2=(
+4)2+t2,PE2=(b-t)2+42,DE2=(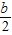 )2+b2,
)2+b2,∵△PDE是等腰直角三角形,
∴PD2=PE2,且PD2+PE2=DE2,
即(
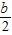 +4)2+t2=(b-t)2+42,且(
+4)2+t2=(b-t)2+42,且(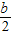 +4)2+t2+(b-t)2+42=(
+4)2+t2+(b-t)2+42=(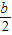 )2+b2,
)2+b2, b2+4b+16+t2=b2-2bt+t2+16,且
b2+4b+16+t2=b2-2bt+t2+16,且 b2+4b+16+t2+b2-2bt+t2+16=
b2+4b+16+t2+b2-2bt+t2+16= b2+b2,
b2+b2,整理得,b=
 (t+2)且t2-b(t-2)+16=0,
(t+2)且t2-b(t-2)+16=0,∴t2-
 (t+2)(t-2)+16=0,
(t+2)(t-2)+16=0,整理得,t2=16,
解得t1=4,t2=-4(舍去),
∴点P的坐标是(4,4);
②PD是斜边时,∵△PDE是等腰直角三角形,
∴PE⊥DE,且PE=DE,
过点P作PF⊥y轴于点F,

∵∠DEO+∠PEO=90°,∠DEO+∠EDO=90°,
∴∠PEO=∠EDO,
在△EDO和△PEF中,
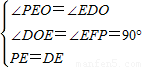 ,
,∴△EDO≌△PEF(AAS),
∴EF=DO=
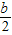 ,PC=EO=b,
,PC=EO=b,又∵点P(4,t),
∴b=4,b-t=
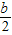 ,
,解得t=
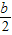 =
= ×4=2,
×4=2,∴点P坐标为(4,2),
此时点C、F重合,点M、N重合,
综上所述,点P的坐标为(4,4)或(4,2).
故答案为:(4,4)或(4,2).
点评:本题是一次函数的综合题型,主要利用了全等三角形的判定与性质,等腰三角形的性质,直线与坐标轴的交点的求解,勾股定理的应用,综合题但难度不大,要注意分情况讨论.

练习册系列答案
相关题目
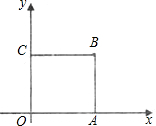 如图,正方形OABC的边长为2,则该正方形绕点O逆时针旋转45°后,B点的坐标为( )
如图,正方形OABC的边长为2,则该正方形绕点O逆时针旋转45°后,B点的坐标为( )| A、(2,2) | ||
B、(0,2
| ||
C、(2
| ||
| D、(0,2) |
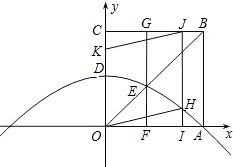 如图,在平面直角坐标系中,正方形OABC的边长是2.O为坐标原点,点A在x的正半轴上,点C在y的正半轴上.一条抛物线经过A点,顶点D是OC的中点.
如图,在平面直角坐标系中,正方形OABC的边长是2.O为坐标原点,点A在x的正半轴上,点C在y的正半轴上.一条抛物线经过A点,顶点D是OC的中点.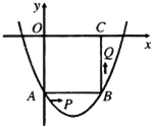 如图在平面直角坐标系xoy中,正方形OABC的边长为2厘米,点A、C分别在y轴的负半轴和x轴的正半轴上.抛物线y=ax2+bx+c经过点A,B和点D(4,
如图在平面直角坐标系xoy中,正方形OABC的边长为2厘米,点A、C分别在y轴的负半轴和x轴的正半轴上.抛物线y=ax2+bx+c经过点A,B和点D(4,
 如图,正方形OABC和正方形AEDF各有一个顶点在一反比例函数图象上,且正方形OABC的边长为2.
如图,正方形OABC和正方形AEDF各有一个顶点在一反比例函数图象上,且正方形OABC的边长为2.