题目内容
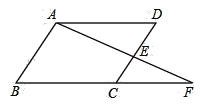
【题目】如图,在ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,S□ABCD=18,则S△ABF=_____.
【答案】18
【解析】
依据已知条件和平行四边形的性质及全等三角形的判定可知∠DAE=∠F,∠D=∠ECF,又DE=CE,所以△AED≌△FEC,所以S△ABF=S平行四边形ABCD,从而求解.
∵四边形ABCD为平行四边形,
∴AD∥BC.
∴∠DAE=∠F,∠D=∠ECF.
∵E是DC的中点,
∴DE=CE.
在△AED和△FEC中,
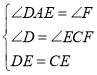 ,
,
∴△AED≌△FEC(AAS).
∴S△AED=S△FEC.
∴S△ABF=S四边形ABCE+S△CEF=S四边形ABCE+S△AED=S平行四边形ABCD=18.
故答案为:18.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目