Question

由直线y=kx+2k-1和直线y=（k+1）x+2k+1（k是正整数）与x轴及y轴所围成的图形面积为S，则S的最小值是

7

4

．

Answer 1

分析：首先用k表示出两条直线与坐标轴的交点坐标，然后表示出围成的面积S，根据得到的函数的取值范围确定其最值即可．

解答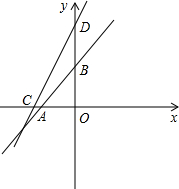：解：y=kx+2k-1恒过（-2，-1），
y=（k+1）x+2k+1也恒过（-2，-1），
k为正整数，那么，k≥1，且k∈Z
如图，
直线y=kx+2k-1与X轴的交点是A（

-(2k-1)

k

，0），与y轴的交点是B（0，2k-1）
直线y=（k+1）x+2k+1与X轴的交点是C（

-(2k+1)

k+1

，0），与y轴的交点是D（0，2k+1），
那么，S_{四边形ABDC}=S_△COD-S_△AOB，
=

1

2

（OC•OD-OA•OB），
=

1

2

[

(2k+1)2

k+1

-

(2k-1)2

k

]，
=

1

2

（4-

1

k2+k

），
=2-

1

2k2+2k

又，k≥1，且k∈Z，
那么，2-

1

2k2+2k

在定义域k≥1上是增函数，
因此，当k=1时，四边形ABDC的面积最小，
最小值S=2-

1

4

=

7

4

．

点评：本题考查了两条指向相交或平行问题，解题的关键是用k表示出直线与坐标轴的交点坐标并用k表示出围成的三角形的面积，从而得到函数关系式，利用函数的知识其最值问题．