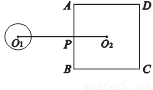
题目内容
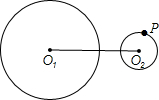如图，⊙O1的半径为4，⊙O2的半径为1，O1O2=6，P为⊙O2上一动点，过P点作⊙O1的切线，则切线长最短为（ ）A、2
| ||
| B、5 | ||
| C、3 | ||
D、3
|
分析：圆心距为6，圆O1的半径为4，圆O2的半径为1，则点P在连心线上；且在O1O2之间时，从点P作圆O1的切线时，切线长最短；设PA与圆O1的切点为A，连接O1A，则∠O1AP=90°，O1A=4，PO1=6-1=5，由勾股定理知AP=3．
解答：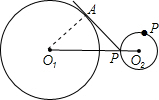
解：设PA与圆O1的切点为A，连接O1A，则∠O1AP=90°，
∵O1A=4，PO1=6-1=5，
∴AP=
=3．
故选C．
解：设PA与圆O1的切点为A，连接O1A，则∠O1AP=90°，∵O1A=4，PO1=6-1=5，
∴AP=
| 25-16 |
故选C．
点评：本题利用了切线的性质，勾股定理求解．
练习册系列答案
相关题目
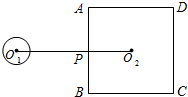11、如图，⊙O1的半径为1，正方形ABCD的边长为6，点O2为正方形ABCD的中心，O1O2垂直AB于P点，O1O2=8．若将⊙O1绕点P按顺时针方向旋转360°，在旋转过程中，⊙O1与正方形ABCD的边只有一个公共点的情况一共出现（ ）
如图，⊙O1的半径为1，正方形ABCD的边长为6，点O2为正方形ABCD中心，O1O2⊥AB于P点，O1O2=8．若将⊙O1绕点P按顺时针方向旋转360°，在旋转过程中，⊙O1与正方形ABCD的边只有一个公共点的情况共出现
