题目内容
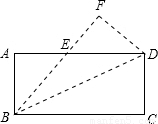
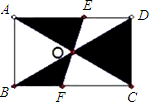如图矩形ABCD的对角线AC和BD相交于点O，过点O的直线分别交AD和BC于点E，F，AB=3，BC=4，则图中阴影部分的面积为________．
6
分析：首先结合矩形的性质证明△AOE≌△COF，得△AOE、△COF的面积相等，从而将阴影部分的面积转化为△BCD的面积．
解答：∵四边形ABCD是矩形，
∴OA=OC，∠AEO=∠CFO；
又∵∠AOE=∠COF，
∴△AOE≌△COF，得S△AOE=S△COF，
∴S阴影=S△AOE+S△BOF+S△COD=S△AOE+S△BOF+S△COD=S△BCD；
∵S△BCD=
BC•CD=6，故S阴影=6．
故答案为6．
点评：此题主要考查了矩形的性质以及全等三角形的判定和性质，能够根据三角形全等，从而将阴影部分的面积转化为矩形面积的一半，是解决问题的关键．
分析：首先结合矩形的性质证明△AOE≌△COF，得△AOE、△COF的面积相等，从而将阴影部分的面积转化为△BCD的面积．
解答：∵四边形ABCD是矩形，
∴OA=OC，∠AEO=∠CFO；
又∵∠AOE=∠COF，
∴△AOE≌△COF，得S△AOE=S△COF，
∴S阴影=S△AOE+S△BOF+S△COD=S△AOE+S△BOF+S△COD=S△BCD；
∵S△BCD=
BC•CD=6，故S阴影=6．故答案为6．
点评：此题主要考查了矩形的性质以及全等三角形的判定和性质，能够根据三角形全等，从而将阴影部分的面积转化为矩形面积的一半，是解决问题的关键．
练习册系列答案
相关题目
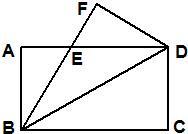14、如图矩形ABCD中BC=8，AB=4，将矩形纸片沿对角线对折，使C点落在F处，BC与AD边交于点E，则下列四个结论中：
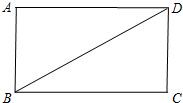如图，已知矩形ABCD．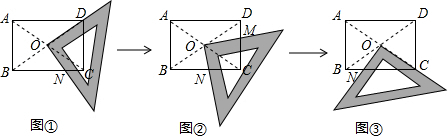
如图矩形ABCD中BC=8，AB=4，将矩形纸片沿对角线对折，使C点落在F处，BC与AD边交于点E，则下列四个结论中：