题目内容
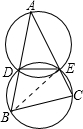
已知△ABC为锐角三角形，⊙O经过点B，C，且与边AB，AC分别相交于点D，E．若⊙O的半径与△ADE的外接圆的半径相等，则⊙O一定经过△ABC的（ ）
| A．内心 | B．外心 | C．重心 | D．垂心 |
如图，连接BE．
因为△ABC为锐角三角形，所以∠BAC，∠ABE均为锐角．
又因为⊙O的半径与△ADE的外接圆的半径相等，且DE为两圆的公共弦，所以∠BAC=∠ABE．
于是，∠BEC=∠BAC+∠ABE=2∠BAC．
若△ABC的外心为O1，则∠BO1C=2∠BAC，
所以⊙O一定过△ABC的外心．
故选B．
因为△ABC为锐角三角形，所以∠BAC，∠ABE均为锐角．
又因为⊙O的半径与△ADE的外接圆的半径相等，且DE为两圆的公共弦，所以∠BAC=∠ABE．
于是，∠BEC=∠BAC+∠ABE=2∠BAC．
若△ABC的外心为O1，则∠BO1C=2∠BAC，
所以⊙O一定过△ABC的外心．
故选B．
练习册系列答案
阅读快车系列答案
相关题目