题目内容
如图,用三个一样的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH,连接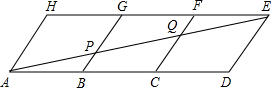 AE,与BG、CF分别交于P、Q.
AE,与BG、CF分别交于P、Q.(1)若AB=9,求线段BP的长;
(2)观察图形,是否有三角形与△ACQ全等?并证明你的结论.
分析:(1)可通过证△ABP∽△ADE,得出关于线段BP的比例关系,然后根据已知条件去求BP的值;
(2)根据菱形的性质及全等三角形的判定方法进行分析,从而不难得到答案.
(2)根据菱形的性质及全等三角形的判定方法进行分析,从而不难得到答案.
解答: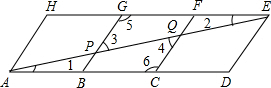 解:(1)∵菱形ABGH、BCFG、CDEF是全等菱形,
解:(1)∵菱形ABGH、BCFG、CDEF是全等菱形,
∴BC=CD=DE=AB=9,
∴AD=3AB=3×9=27,
∵BG∥DE,
∴∠ABG=∠D,∠APB=∠AED,
∴△ABP∽△ADE,
∴
=
,
∴BP=
•DE=
×9=3;
(2)图中的△EGP与△ACQ全等.
∵菱形ABGH、BCFG、CDEF是全等的菱形,
∴AB=BC=EF=FG,
∴AB+BC=EF+FG,
∴AC=EG,
∵AD∥HE,
∴∠1=∠2,
∵BG∥CF,
∴∠3=∠4,
∴△EGP≌△ACQ.
 解:(1)∵菱形ABGH、BCFG、CDEF是全等菱形,
解:(1)∵菱形ABGH、BCFG、CDEF是全等菱形,∴BC=CD=DE=AB=9,
∴AD=3AB=3×9=27,
∵BG∥DE,
∴∠ABG=∠D,∠APB=∠AED,
∴△ABP∽△ADE,
∴
| BP |
| DE |
| AB |
| AD |
∴BP=
| AB |
| AD |
| 9 |
| 27 |
(2)图中的△EGP与△ACQ全等.
∵菱形ABGH、BCFG、CDEF是全等的菱形,
∴AB=BC=EF=FG,
∴AB+BC=EF+FG,
∴AC=EG,
∵AD∥HE,
∴∠1=∠2,
∵BG∥CF,
∴∠3=∠4,
∴△EGP≌△ACQ.
点评:此题考查全等三角形的判定,相似三角形的性质及菱形的性质等知识点的综合运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

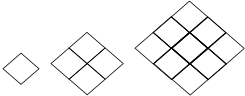 如图,用火柴棒摆菱形,请你通过观察探究:菱形的个数的增长规律与火柴棒的根数的增长规律.
如图,用火柴棒摆菱形,请你通过观察探究:菱形的个数的增长规律与火柴棒的根数的增长规律.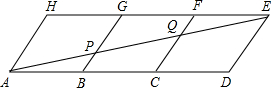 AE,与BG、CF分别交于P、Q.
AE,与BG、CF分别交于P、Q.