题目内容
【题目】如图1,平面直角坐标系x0y中,点A(0,2),B(1,0),C(﹣4,0)点D为射线AC上一动点,连结BD,交y轴于点F,⊙M是△ABD的外接圆,过点D的切线交x轴于点E.
(1)判断△ABC的形状;
(2)当点D在线段AC上时,
①证明:△CDE∽△ABF;
②如图2,⊙M与y轴的另一交点为N,连结DN、BN,当四边形ABND为矩形时,求tan∠DBC;
(3)点D在射线AC运动过程中,若![]() ,求
,求![]() 的值.
的值.

【答案】(1)直角三角形;(2)①证明见解析,②![]() ;(3)
;(3)![]() 或
或![]()
【解析】试题分析:(1)已知三个点的坐标,可以求出相应线段的长度,运用三角函数可以证明∠ACO=∠BAO,进一步证明∠BAC=90°;
(2)只需证明∠CDE=∠ABD,∠DCE=∠BAF,即可证明相似;
当四边形ABND为矩形时,根据直角三角形AOB和直角三角形ABN相似,可求AN长度,进一步求出OM,运用三角函数求解即可;
(3)根据点D在线段AC上,和线段AC的延长线上分别讨论求解;
试题解析:
解:由点A(0,2),B(1,0),C(﹣4,0)可知:OA=2,OC=4,OB=1,
在直角三角形AOC和直角三角形AOB中,根据勾股定理可求:AC=![]() =2
=2![]() ,
,
AB=![]() =
=![]() .
.
(1)在直角三角形AOC和直角三角形AOB中,tan∠ACO=![]() ,tan∠BAO=
,tan∠BAO=![]() ,所以∠ACO=∠BAO,
,所以∠ACO=∠BAO,
∵∠ACO+∠CAO=90°,
∴∠BAO+∠CAO=90°,∠BAC=90°,
∴△ABC是直角三角形.
(2)①由(1)知:∠BAC=90°,∴BD是圆M的直径,
∵DE是圆M的切线,∴∠BDE=90°.
∴∠CDE+∠ADB=90°,又∠ADB+∠ABD=90°,∴∠CDE=∠ABD,
∵∠DCE+∠ABO=90°,∠ABO+∠BAF=90°,∴∠DCE=∠BAF
∴△CDE∽△ABF.
②当四边形ABND为矩形时,∵∠ABN=90°,∴AN是圆的直径,由OB是直角三角形ABN的斜边上的高线,由∠BAO=∠BA0,∠BOA=∠ABN=90°,
∴△AOB∽△ABN,
∴![]() , ∴AB2=OA×AN,
, ∴AB2=OA×AN,
∵OA=2,AB=![]() ,可求:AN=
,可求:AN=![]() ,
,
∴ON=![]() ,OM=MN﹣ON=
,OM=MN﹣ON=![]() ,
,
在直角三角形OBN中,
tan∠DBC=![]() =
=![]() .
.
(3)若点D 在线段AC上,
如图2:由①知△CDE∽△ABF可得: ![]() ,AC=2
,AC=2![]() ,
,
由![]() ,可得:CD=
,可得:CD=![]() ,AD=
,AD=![]() ,
,
在直角三角形ABD中,由勾股定理可求:BD=![]() =
=![]() ,
,
∵∠CBD=∠FBO,∠BOF=∠BDE=90°,
∴△BFO∽△BED,
∴![]() ,
,
设:DE=2x,则BF=3x,由勾股定理得:OF=![]() =
=![]() ,
,
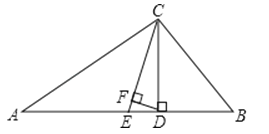
∴ ,解得:
,解得: ![]() ,
,
∴DE=![]() ,BF=
,BF=![]() ,DF=BD﹣DF=
,DF=BD﹣DF=![]() ,
,
∴![]() =
=![]() ,
,
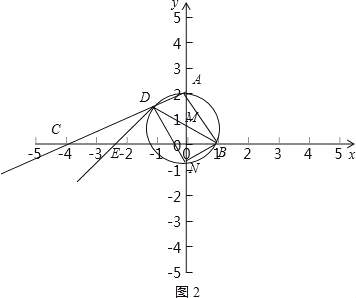
若点D在线段AC的延长线上,
如图3:∵DE是圆M的切线,
∴∠BDE=90°
∴∠EDC+∠CDB=90°
∵∠ABD+∠CDB=90°
∴∠EDC=∠ABD,
∵∠DEB+∠DBE=90°,∠DBE+∠OFB=90°
∴∠DEB=∠OFB,
∴△CDE∽△ABF,可得: ![]() ,AC=2
,AC=2![]() ,
,
由![]() ,可得:CD=
,可得:CD=![]() ,∴AD=AC+CD=
,∴AD=AC+CD=![]() ,
,
由勾股定理得:BD=![]() =
=![]() ,
,
∵∠CBD=∠FBO,∠BOF=∠BDE=90°,
∴△BFO∽△BED,
∴![]() ,
,
设:DE=2x,则BF=3x,
由勾股定理得:OF=![]() =
=![]() ,
,
∴ ,解得:
,解得: ![]() ,
,
∴DE=2x=![]() ,BF=3x=
,BF=3x=![]() ,DF=BD﹣DF=
,DF=BD﹣DF=![]() ,
,
∴![]() =
=![]() ,
,
综上所述: ![]() 的值是
的值是![]() 或
或![]() .
.

图3

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案