题目内容
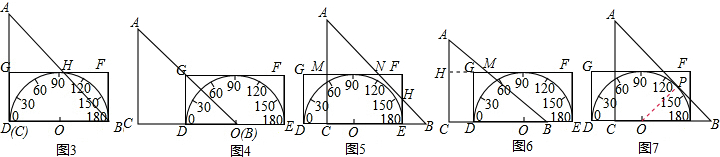
如图(1),形如三角板的△ABC中,∠ACB=90°,∠ABC=45°,BC=12cm,形如矩形量角器的半圆O的直径DE=12cm,矩形DEFG的宽EF=6cm,矩形量角器以2cm/s的速度从 左向右运动,在运动过程中,点D、E始终在BC所在的直线上,设运动时间为x(s),矩形量角器和△ABC的重叠部分的面积为S(cm2).当x=0(s)时,点E与点C重合.
(1)当x=3时,如图(2),S=
(2)求S关于x的函数关系式;
(3)当x为何值时,△ABC的斜边所在的直线与半圆O所在的圆相切?
(1)当x=3时,如图(2),S=
36
36
cm2,当x=6时,S=54
54
cm2,当x=9时,S=18
18
cm2;(2)求S关于x的函数关系式;
(3)当x为何值时,△ABC的斜边所在的直线与半圆O所在的圆相切?

分析:(1)根据题意画图图形,然后由矩形的面积公式或者进行计算;
(2)当3<x<6时,重叠部分是不规则的四边形,不能直接用x表示,要采用面积的分割法来求,先求S△ABC,S△AMN,再求S△BEH,然后求重叠部分的面积;当6<x<9时,重叠部分也是不规则的四边形,也采用面积的分割法来求,先求S△ABC,S△AHM,再求S四边形HGDC,这样才能求出S与x的函数关系式;
(3)切点在线段AB上,利用切线的性质和等腰直角三角形的性质进行解答.
(2)当3<x<6时,重叠部分是不规则的四边形,不能直接用x表示,要采用面积的分割法来求,先求S△ABC,S△AMN,再求S△BEH,然后求重叠部分的面积;当6<x<9时,重叠部分也是不规则的四边形,也采用面积的分割法来求,先求S△ABC,S△AHM,再求S四边形HGDC,这样才能求出S与x的函数关系式;
(3)切点在线段AB上,利用切线的性质和等腰直角三角形的性质进行解答.
解答:解:(1)当x=3时,CE=6cm.如图2所示,则S=CE•EF=6×6=36(cm2);
当x=6时,CE=12cm.如图3所示,易证GH是△ACB的中位线,阴影部分为四边形GHBD,四边形GHBD为直角梯形,则
S=
×GD=
×6=54(cm2)
当x=9时,CE=18cm.如图4所示,易证阴影部分△GDO是等腰直角三角形,则S=
OD•GD=
×6×6=18(cm2).
故答案分别是:36;54;18;
(2)①如图5,设矩形DEFG与斜边AB的交点分别为N、H,与直角边AC的交点为M;
∵BE=12-2x,AM=12-6=6,
∴S=S△ABC-S△AMN-S△BHE=
×12×12-
×6×6-
×(12-2x)2=-2x2+24x-18,
∴当3<x<6时,S=-2x2+24x-18.
②如图6,设矩形DEFG与斜边AB的交点为M,延长FG交AC于点H;
∵AH=12-6=6,HG=2x-12,
∴S=S△ABC-S△AHM-S矩形HCDG=
×12×12-
×6×6-
×6×(2x-12)=-12x+126,
∴当6<x<9时,S=-12x+126.
综上所述,S=
;
(3)如图7,过点O作OD⊥AB于点P,由题意得OP=6cm;
∵∠ABC=45°,∠OPB=90°,
∴OB=
OP=6
cm,
∴x=
=9-3
(s);
当x=6时,CE=12cm.如图3所示,易证GH是△ACB的中位线,阴影部分为四边形GHBD,四边形GHBD为直角梯形,则
S=
| GH+CE |
| 2 |
| 6+12 |
| 2 |
当x=9时,CE=18cm.如图4所示,易证阴影部分△GDO是等腰直角三角形,则S=
| 1 |
| 2 |
| 1 |
| 2 |
故答案分别是:36;54;18;
(2)①如图5,设矩形DEFG与斜边AB的交点分别为N、H,与直角边AC的交点为M;
∵BE=12-2x,AM=12-6=6,
∴S=S△ABC-S△AMN-S△BHE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴当3<x<6时,S=-2x2+24x-18.
②如图6,设矩形DEFG与斜边AB的交点为M,延长FG交AC于点H;
∵AH=12-6=6,HG=2x-12,
∴S=S△ABC-S△AHM-S矩形HCDG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴当6<x<9时,S=-12x+126.
综上所述,S=
|
(3)如图7,过点O作OD⊥AB于点P,由题意得OP=6cm;
∵∠ABC=45°,∠OPB=90°,
∴OB=
| 2 |
| 2 |
∴x=
6+12-6
| ||
| 2 |
| 2 |

点评:本题考查了圆的综合题.解题时,把求函数关系式与三角形的有关知识有机结合起来,综合性比较强.对于这类动点问题,一定要分类讨论,以防漏解或错解.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
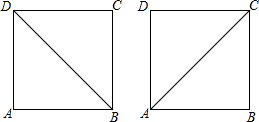 用对角线把多边形分成几个三角形,叫做“多边形的三角剖分”.如图,凸四边形ABCD,有两种剖分方法:(如图示)20世纪,数学家乌尔班发现并证明了下面的公式:
用对角线把多边形分成几个三角形,叫做“多边形的三角剖分”.如图,凸四边形ABCD,有两种剖分方法:(如图示)20世纪,数学家乌尔班发现并证明了下面的公式: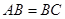 ,且
,且 ),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).
),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).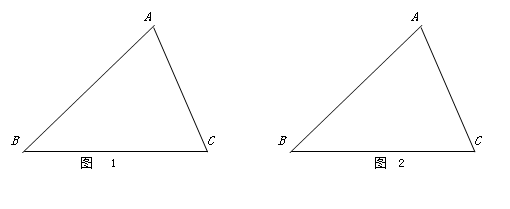 (1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”,从而平分蛋糕.
(1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”,从而平分蛋糕. 个图案中正三角
个图案中正三角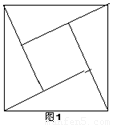
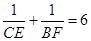 ,则等边三角
,则等边三角
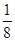 B.
B. 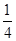 C.
C.
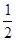 D.1
D.1