题目内容
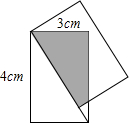 把两个相同的矩形按如图所示的方式叠合起来,重叠部分为图中的阴影部分,已知矩形的长与宽分别为4cm与3cm,则重叠部分的面积为________cm2.
把两个相同的矩形按如图所示的方式叠合起来,重叠部分为图中的阴影部分,已知矩形的长与宽分别为4cm与3cm,则重叠部分的面积为________cm2.
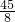
分析:根据勾股定理求出AC,求出AE,证△AEF∽△ABC,根据相似三角形的相似比等于对应高之比求出
 =
= ,求出S四边形CBFE=
,求出S四边形CBFE=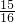 S△ABC,代入求出即可.
S△ABC,代入求出即可.解答:

∵BC=3,AB=4,在Rt△ABC中,由勾股定理得:AC=
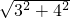 =5,
=5,∴AE=AC-CE=5-4=1
由矩形的性质得:∠AEF=∠CBA=90°,
∵∠FAE=∠CAB,
∴△AEF∽△ABC,
∴
 =
= =
=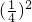 =
= ,
,∴S四边形CBFE=
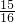 S△ABC=
S△ABC=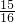 ×
× ×3×4=
×3×4=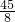 ,
,故答案为:
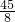 .
.点评:本题考查了相似三角形的性质和判定,三角形的面积,勾股定理,矩形的性质等知识点,主要考查学生的计算能力注意:相似三角形的面积比等于相似比的平方.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
 (2012•海门市模拟)把两个相同的矩形按如图所示的方式叠合起来,重叠部分为图中的阴影部分,已知矩形的长与宽分别为4cm与3cm,则重叠部分的面积为
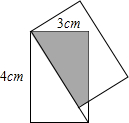
(2012•海门市模拟)把两个相同的矩形按如图所示的方式叠合起来,重叠部分为图中的阴影部分,已知矩形的长与宽分别为4cm与3cm,则重叠部分的面积为 (2012•鼓楼区一模)把两个相同的矩形按如图所示的方式叠合起来,若它们的长与宽分别为48cm与36cm,则重叠部分的面积为
(2012•鼓楼区一模)把两个相同的矩形按如图所示的方式叠合起来,若它们的长与宽分别为48cm与36cm,则重叠部分的面积为

