题目内容
已知关于 的一元二次方程
的一元二次方程 有实数根,
有实数根, 为正整数.
为正整数.
(1)求 的值;
的值;
(2)当此方程有两个不为0的整数根时,将关于 的二次函数
的二次函数 的图象向下平移2个单位,求平移后的函数图象的解析式;
的图象向下平移2个单位,求平移后的函数图象的解析式;
(3)在(2)的条件下,将平移后的二次函数图象位于 轴左侧的部分沿
轴左侧的部分沿 轴翻折,图象的其余部分保持不变,得到一个新的图象G.当直线
轴翻折,图象的其余部分保持不变,得到一个新的图象G.当直线 与图象G有3个公共点时,请你直接写出
与图象G有3个公共点时,请你直接写出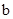 的取值范围.
的取值范围.

 的一元二次方程
的一元二次方程 有实数根,
有实数根, 为正整数.
为正整数.(1)求
 的值;
的值;(2)当此方程有两个不为0的整数根时,将关于
 的二次函数
的二次函数 的图象向下平移2个单位,求平移后的函数图象的解析式;
的图象向下平移2个单位,求平移后的函数图象的解析式;(3)在(2)的条件下,将平移后的二次函数图象位于
 轴左侧的部分沿
轴左侧的部分沿 轴翻折,图象的其余部分保持不变,得到一个新的图象G.当直线
轴翻折,图象的其余部分保持不变,得到一个新的图象G.当直线 与图象G有3个公共点时,请你直接写出
与图象G有3个公共点时,请你直接写出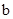 的取值范围.
的取值范围.
(1) 1,2,3;(2)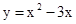 ;(3)
;(3)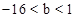 .
.
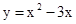 ;(3)
;(3)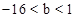 .
.试题分析:(1)由
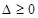 求出正整数解即可.
求出正整数解即可.(2)求出方程有两个不为0的整数根时的二次函数解析式,根据平移的性质得到平移后的函数图象的解析式.
(3)分直线
 与
与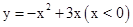 有一个交点且与
有一个交点且与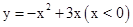 有两个交点和直线
有两个交点和直线 与
与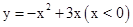 有两个交点且与
有两个交点且与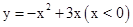 有一个交点两种情况求解即可.
有一个交点两种情况求解即可.(1)∵ 方程有实数根,∴
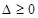 .
.∴
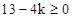 ,解得
,解得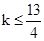 .
.∵
 为正整数,∴
为正整数,∴ 为1,2,3.
为1,2,3.(2)当
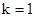 时,
时,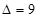 ,方程的两个整数根为6,0;
,方程的两个整数根为6,0;当
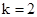 时,
时,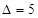 ,方程无整数根;
,方程无整数根;当
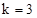 时,
时,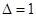 ,方程的两个整数根为2,1
,方程的两个整数根为2,1∴
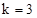 ,原抛物线的解析式为:
,原抛物线的解析式为: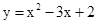 .
.∴平移后的图象的解析式为
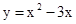 .
.(3)翻折后得到一个新的图象G的解析式为
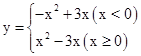 ,
,联立
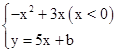 得
得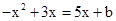 ,即
,即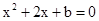 .
.由
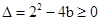 得
得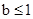 .
.∴当
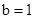 或
或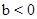 时,直线
时,直线 与
与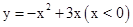 有一个交点,当
有一个交点,当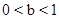 时,直线
时,直线 与
与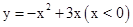 有两个交点.
有两个交点.联立
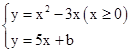 得
得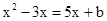 ,即
,即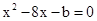 .
.由
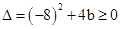 得
得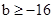 .
.∴当
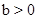 或
或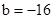 时,直线
时,直线 与
与 有一个交点,当
有一个交点,当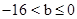 时,直线
时,直线 与
与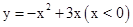 有两个交点.
有两个交点.∴要使直线
 与图象G有3个公共点即要直线
与图象G有3个公共点即要直线 与
与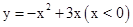 有一个交点且与
有一个交点且与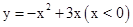 有两个交点;或直线
有两个交点;或直线 与
与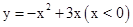 有两个交点且与
有两个交点且与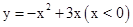 有一个交点.
有一个交点.∴
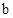 的取值范围为
的取值范围为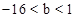 .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 )三点.
)三点.
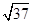 ,一抛物线过点A、B、 C.
,一抛物线过点A、B、 C.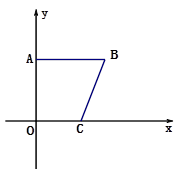

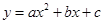
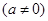 中的
中的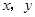 满足下表:
满足下表: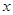
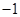
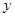
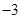
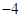
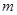
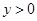 时的
时的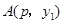 ,
,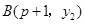 两点都在该函数图象上,且
两点都在该函数图象上,且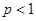 ,试比较
,试比较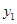 与
与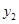 的大小.
的大小.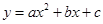 (
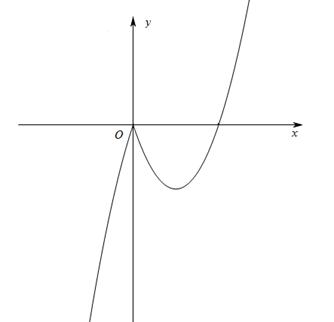
(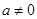 )的图象如图所示,对称轴是直线
)的图象如图所示,对称轴是直线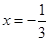 ,有下列结论:①
,有下列结论:①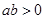 ;②
;②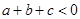 ;③
;③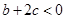 ;④
;④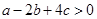 .其中正确结论的个数是( ).
.其中正确结论的个数是( ).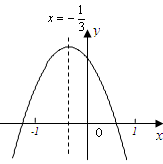
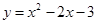 配方后为
配方后为 ,则
,则 .
.