Question

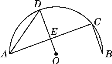
【题目】如图，AB是半圆O的直径，C，D是半圆O上的两点，OD∥BC，OD与AC交于点E.

(1)若∠D＝70°，求∠CAD的度数；

(2)若AC＝8，DE＝2，求AB的长．

Answer 1

【答案】(1) 20°；(2) 10.

【解析】

（1）根据圆周角定理可得∠ACB=90°，则∠CAB的度数即可求得，在等腰△AOD中，根据等边对等角求得∠DAO的度数，则∠CAD即可求得；

（2）设OA＝x，则OE＝OD－DE＝x－2. 在Rt△OAE中利用勾股定理即可求解.

解：(1)∵OA＝OD，∠D＝70°，

∴∠OAD＝∠D＝70°.

∴∠AOD＝180°－∠OAD－∠D＝40°.

∵AB是半圆O的直径，

∴∠C＝90°.

∵OD∥BC，

∴∠AEO＝∠C＝90°，即OD⊥AC.

∴＝.

∴∠CAD＝∠AOD＝20°.

(2)由(1)可知OD⊥AC，

∴AE＝AC＝×8＝4.

设OA＝x，则OE＝OD－DE＝x－2.

在Rt△OAE中，OE2＋AE2＝OA2，

即(x－2)2＋42＝x2，解得x＝5.

∴AB＝2OA＝10.