题目内容
计算:
(1)(-a3)2•(-a2)3;
(2)-t3•(-t)4•(-t)5;
(3)(1
)2006×(-0.6)2007;
(4)(-
)-1+(-2)2×50-(
)-2;
(5)(
)-2-23×0.125+20120+|-1|;
(6)(p-q)4÷(q-p)3•(p-q)2.
(1)(-a3)2•(-a2)3;
(2)-t3•(-t)4•(-t)5;
(3)(1
| 2 |
| 3 |
(4)(-
| 1 |
| 4 |
| 1 |
| 2 |
(5)(
| 1 |
| 2 |
(6)(p-q)4÷(q-p)3•(p-q)2.
考点:整式的混合运算,零指数幂,负整数指数幂
专题:计算题
分析:(1)(2)(3)(6)利用同底数幂的乘法,幂的乘方计算即可;
(4)(5)先算乘方、负指数幂、0指数幂,再算乘除,最后算加减.
(4)(5)先算乘方、负指数幂、0指数幂,再算乘除,最后算加减.
解答:解:(1)原式=a6•(-a6)
=-a12;
(2)原式=-t3•t4•(-t5)
=t12;
(3)原式=[
×(-0.6)]2006×(-0.6)
=1×(-0.6)
=-0.6;
(4)原式=-4+4×1-4
=-4;
(5)原式=4-8×0.125+1+1
=4-1+1+1
=5;
(6)原式=-(p-q)•(p-q)2
=(p-q)3.
=-a12;
(2)原式=-t3•t4•(-t5)
=t12;
(3)原式=[
| 5 |
| 3 |
=1×(-0.6)
=-0.6;
(4)原式=-4+4×1-4
=-4;
(5)原式=4-8×0.125+1+1
=4-1+1+1
=5;
(6)原式=-(p-q)•(p-q)2
=(p-q)3.
点评:此题考查整式的混合运算,掌握运算方法和运算符号的确定是正确计算的关键.

练习册系列答案
相关题目
 如图,将△ABC绕着点O顺时针旋转90°后得到△A1B1C1,画出旋转后的△A1B1C1.
如图,将△ABC绕着点O顺时针旋转90°后得到△A1B1C1,画出旋转后的△A1B1C1.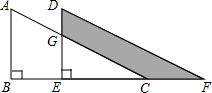 如图,将直角三角形ABC沿射线BC的方向平移得到三角形DEF.设图中,AB=8,BE=5,GE=5,求图中阴影部分的面积.
如图,将直角三角形ABC沿射线BC的方向平移得到三角形DEF.设图中,AB=8,BE=5,GE=5,求图中阴影部分的面积.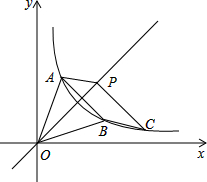 如图,在平面直角坐标系中,△AOB的顶点O是坐标原点,点A的坐标为(1,3),A、B两点关于直线y=x对称,反比例函数y=
如图,在平面直角坐标系中,△AOB的顶点O是坐标原点,点A的坐标为(1,3),A、B两点关于直线y=x对称,反比例函数y=