题目内容
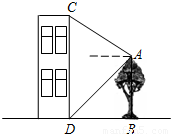
五月石榴红,枝头鸟儿歌.一只小鸟从石榴树上的A处沿直线飞到对面一房屋的顶部C处.从A处看房屋顶部C处的仰角为30°,看房屋底部D处的俯角为45°,石榴树与该房屋之间的水平距离为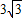 米,求出小鸟飞行的距离AC和房屋的高度CD.
米,求出小鸟飞行的距离AC和房屋的高度CD.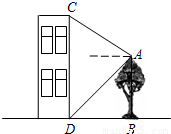
【答案】分析:首先分析图形:根据题意构造直角三角形.本题涉及到两个直角三角形△ACE、△AED,应利用其等边DE=AE构造方程关系式,进而可解即可求出答案.
解答: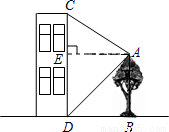 解:作AE⊥CD于点E.
解:作AE⊥CD于点E.
由题意可知:∠CAE=30°,∠EAD=45°,AE=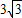 米.
米.
在Rt△ACE中,tan∠CAE=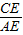 ,即tan30°=
,即tan30°= .
.
∴CE=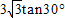 =
=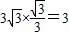 (米),
(米),
∴AC=2CE=2×3=6(米).
在Rt△AED中,∠ADE=90°-∠EAD=90°-45°=45°,
∴DE=AE=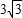 (米).
(米).
∴DC=CE+DE=(3+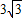 )米.
)米.
答:AC=6米,DC=(3+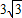 )米.
)米.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
解答:
 解:作AE⊥CD于点E.
解:作AE⊥CD于点E.由题意可知:∠CAE=30°,∠EAD=45°,AE=
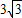 米.
米.在Rt△ACE中,tan∠CAE=
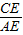 ,即tan30°=
,即tan30°= .
.∴CE=
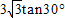 =
=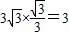 (米),
(米),∴AC=2CE=2×3=6(米).
在Rt△AED中,∠ADE=90°-∠EAD=90°-45°=45°,
∴DE=AE=
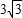 (米).
(米).∴DC=CE+DE=(3+
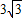 )米.
)米.答:AC=6米,DC=(3+
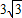 )米.
)米.点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
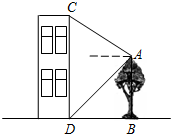 水平距离为
水平距离为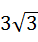 米,求出小鸟飞行的距离AC和房屋的高度CD.
米,求出小鸟飞行的距离AC和房屋的高度CD.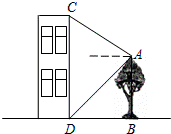
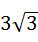 米,求出小鸟飞行的距离AC和房屋的高度CD.
米,求出小鸟飞行的距离AC和房屋的高度CD.
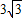 米,求出小鸟飞行的距离AC和房屋的高度CD.
米,求出小鸟飞行的距离AC和房屋的高度CD.