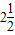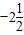题目内容
已知2x2-3xy+y2=0(xy≠0),则
+
的值是( )
| x |
| y |
| y |
| x |
A、2,2
| ||
| B、2 | ||
C、2
| ||
D、-2,-2
|
分析:对等式两边同时除以x2,得(
)2-3
+2=0,解方程可得
=1或2,即
=1或
,即得
+
=2或2
.
| y |
| x |
| y |
| x |
| y |
| x |
| x |
| y |
| 1 |
| 2 |
| x |
| y |
| y |
| x |
| 1 |
| 2 |
解答:解:根据题意,2x2-3xy+y2=0,且xy≠0,
故有(
)2-3
+2=0,
即(
-1)(
-2)=0,
即得
=1或2,故
=1或
,
所以
+
=2或2
.
故选A.
故有(
| y |
| x |
| y |
| x |
即(
| y |
| x |
| y |
| x |
即得
| y |
| x |
| x |
| y |
| 1 |
| 2 |
所以
| x |
| y |
| y |
| x |
| 1 |
| 2 |
故选A.
点评:本题主要考查的是利用因式分解法求解方程,要求学生能够熟练掌握这种解题方法.

练习册系列答案
相关题目
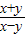 的值为 .
的值为 .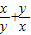 的值是( )
的值是( )