题目内容
【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE;
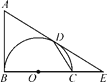
【答案】证明见解析
【解析】
(1)如图,连接OD,BD,
∵AB是⊙O的切线,∴AB⊥BC,即∠ABC=90°,
∵AB=AD,∴∠ABD=∠ADB,
∵OB=OD,∴∠DBO=∠BDO,∴∠ABD+∠DBO=∠ADB+∠BDO,
∴∠ADO=∠ABO=90°,∴AD是半圆O的切线.
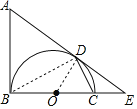
(2)由(1)知,∠ADO=∠ABO=90°,
∴∠A=360°–∠ADO–∠ABO–∠BOD=180°–∠BOD=∠DOC,
∵AD是半圆O的切线,∴∠ODE=90°,∴∠ODC+∠CDE=90°,
∵BC是⊙O的直径,∴∠ODC+∠BDO=90°,∴∠BDO=∠CDE,
∵∠BDO=∠OBD,∴∠DOC=2∠BDO,∴∠DOC=2∠CDE,
∴∠A=2∠CDE.

练习册系列答案
相关题目