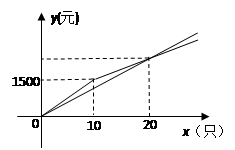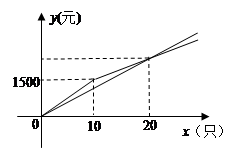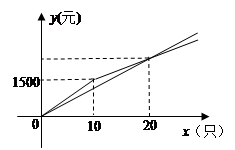Question

某位市民想为贫困山区的孩子们献一份爱心，准备购买一批书包捐赠给他们、经调查有这样的一种书包，原售价为每只150元，现A、B两家商店优惠出售，A商店一律8折出售；B商店规定：购买少于n只的书包，仍以原价出售，超过n只，其中n只书包的部分仍以原价出售，超过n只的部分，打a折出售．在A、B两商店购买x只书包所需的金额分别为y₁（元）和y₂（元），y₁，y₂与x的函数的图象如图所示．
（1）根据图象，可知a=_

6

，n=

10

；
（2）求y₁，y₂关于x的函数解析式；
（3）由于颜色等原因，现该市民在A、B两商店共购买50只这种书包，共付款6240元，问他在A、B两家商店各购买书包多少只？

Answer 1

分析：（1）根据图象以及A商店一律8折出售得出n的值，以及利用两图象有交点得出交点坐标，得出a的值即可；
（2）利用图象上点的坐标，利用待定系数法求一次函数解析式即可；
（3）设B商店购买书包a只，则A商店购买书包（50-a）只，再分当0≤a≤10时，当a＞10时两种情况，分别求出即可．

解答：解：（1）根据图象当购买书包10只，价格为1500元，则n=10，
当n=20时，两图象有交点，得出150×0.8×20=120×20=2400（元），
2400-1500=900，
10×150x=900，
解得：x=0.6，
故a=6，n=10；
故答案为：6，10；

（2）A：设y₁=kx，150×0.8=120，
故y₁=120x，
即B两商店购买x只书包所需的金额分别为y₂（元）的解析式为：y₂=kx+b，
将（10，1500），（20，2400）代入得出：

10k+b=1500 20k+b=2400

，
解得：

k=90 b=600

，
B：y₂=90x+600；

（3）设B商店购买书包a只，则A商店购买书包（50-a）只，
当0≤a≤10时，
150a+120（50-a）=6240，
解得：a=8，
当a＞10时  90a+600+120（50-a）=6240，
解得：a=12，
答：A家商店买42只，B家商店买8只，或A家商店买38只，B家商店买12只．

点评：本题考查了一次函数的应用以及待定系数法求一次函数解析式，结合实际意义得出点的坐标得出是解题关键．