题目内容
(2006•安徽)某公司年初推出一种高新技术产品,该产品销售的累积利润y(万元)与销售时间x(月)之间的关系(即前x个月的利润总和y与x之间的关系)为y= x2-2x(x>0).
x2-2x(x>0).(1)求出这个函数图象的顶点坐标和对称轴;
(2)请在所给坐标系中,画出这个函数图象的简图;
(3)根据函数图象,你能否判断出公司的这种新产品销售累积利润是从什么时间开始盈利的?
(4)这个公司第6个月所获的利润是多少?
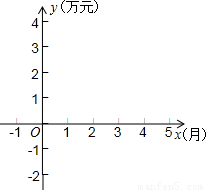
【答案】分析:本题是实际问题与二次函数,画函数图象时,要抓住几个关键点,开口方向,顶点及对称轴,与x轴的交点等等;实际问题中的抛物线图形一般不是完整的图形,受自变量取值范围的限制.
解答: 解:(1)由y=
解:(1)由y= (x2-4x)=
(x2-4x)= (x-2)2-2.
(x-2)2-2.
故函数图象的顶点坐标为(2,-2),对称轴为直线x=2.
(2)如图.
(3)从函数图象可以看出,从4月份开始新产品的销售累积利润盈利.
(4)x=6时,y= ×62-2×6=6,6-2.5=3.5.
×62-2×6=6,6-2.5=3.5.
故这个公司第6个月所获的利润是3.5万元.
点评:一个准确的函数图象,可以为回答问题提供答案,(3)实际上就是什么时候y>0,即盈利.
解答:
 解:(1)由y=
解:(1)由y= (x2-4x)=
(x2-4x)= (x-2)2-2.
(x-2)2-2.故函数图象的顶点坐标为(2,-2),对称轴为直线x=2.
(2)如图.
(3)从函数图象可以看出,从4月份开始新产品的销售累积利润盈利.
(4)x=6时,y=
 ×62-2×6=6,6-2.5=3.5.
×62-2×6=6,6-2.5=3.5.故这个公司第6个月所获的利润是3.5万元.
点评:一个准确的函数图象,可以为回答问题提供答案,(3)实际上就是什么时候y>0,即盈利.

练习册系列答案
相关题目
(2006•安徽)某水果公司以2元/千克的单价新进了10000千克柑橘,为了合理定出销售价格,水果公司需将运输中损失的水果成本折算到没有损坏的水果售价中.销售人员从柑橘中随机抽取若干柑橘统计柑橘损坏情况,结果如下表.如果公司希望全部售完这批柑橘能够获得5000元利润,那么在出售柑橘时,每千克大约定价 元.(结果精确到0.1元)
| 柑橘质量(千克) | 50 | 200 | 500 |
| 损坏的质量(千克) | 5.50 | 19.42 | 51.54 |
(2006•安徽)某水果公司以2元/千克的单价新进了10000千克柑橘,为了合理定出销售价格,水果公司需将运输中损失的水果成本折算到没有损坏的水果售价中.销售人员从柑橘中随机抽取若干柑橘统计柑橘损坏情况,结果如下表.如果公司希望全部售完这批柑橘能够获得5000元利润,那么在出售柑橘时,每千克大约定价 元.(结果精确到0.1元)
| 柑橘质量(千克) | 50 | 200 | 500 |
| 损坏的质量(千克) | 5.50 | 19.42 | 51.54 |
(2006•安徽)某水果公司以2元/千克的进价新进了10 000千克柑橘,为了合理定出销售价格,水果公司在出售前要估算出在运输中可能损坏的水果总质量,以便将损坏的水果成本折算到没有损坏的水果售价中.销售人员首先从所有的柑橘中随机地抽取若干柑橘进行“柑橘损坏率”统计,获得的数据记录如下表(单位:千克):
(1)上表“柑橘损坏的频率”一栏中的五个数据,众数是______;中位数是______;平均数是______.
(2)如果公司希望售完这些柑橘并获利5 000元,则出售这些柑橘时,每千克大约定价为多少元比较合适?(精确到0.1)
| 抽取柑橘的质量(n) | 100 | 200 | 300 | 400 | 500 |
| 损坏柑橘的质量(m) | 10.16 | 19.96 | 30.93 | 41.24 | 19.95 |
| 柑橘损坏的频率(m/n) | 0.1016 | 0.0998 | 0.1031 | 0.1031 | 0.0999 |
(2)如果公司希望售完这些柑橘并获利5 000元,则出售这些柑橘时,每千克大约定价为多少元比较合适?(精确到0.1)
 x2-2x(x>0).
x2-2x(x>0).