题目内容
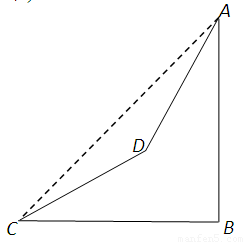
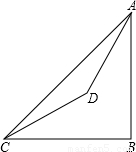
已知:如图,在山脚的C处测得山顶A的仰角为45°,沿着坡度为30°的斜坡前进400米到D处(即∠DCB=30°,CD=400米),测得A的仰角为60°,求山的高度AB.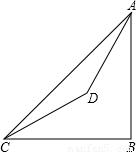
【答案】分析:首先根据题意分析图形;作DE⊥AB于E,作DF⊥BC于F,构造两个直角三角形,分别求解可得DF与EA的值,再利用图形关系,进而可求出答案.
解答: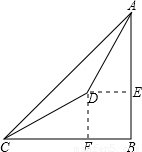 解:作DE⊥AB于E,作DF⊥BC于F,在Rt△CDF中∠DCF=30°,CD=400米,
解:作DE⊥AB于E,作DF⊥BC于F,在Rt△CDF中∠DCF=30°,CD=400米,
∴DF=CD•sin30°= ×400=200(米)
×400=200(米)
CF=CD•cos30°=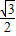 ×400=200
×400=200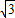 (米)
(米)
在Rt△ADE中,∠ADE=60°,设DE=x米,
∴AE=tan60°•x=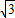 x(米)
x(米)
在矩形DEBF中,BE=DF=200米,
在Rt△ACB中,∠ACB=45°,
∴AB=BC,
即: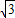 x+200=200
x+200=200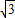 +x
+x
∴x=200,∴AB=AE+BE=(200 +200)米.
+200)米.
点评:命题立意:此题主要考查解直角三角形的相关知识.
解答:
 解:作DE⊥AB于E,作DF⊥BC于F,在Rt△CDF中∠DCF=30°,CD=400米,
解:作DE⊥AB于E,作DF⊥BC于F,在Rt△CDF中∠DCF=30°,CD=400米,∴DF=CD•sin30°=
 ×400=200(米)
×400=200(米)CF=CD•cos30°=
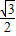 ×400=200
×400=200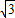 (米)
(米)在Rt△ADE中,∠ADE=60°,设DE=x米,
∴AE=tan60°•x=
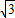 x(米)
x(米)在矩形DEBF中,BE=DF=200米,
在Rt△ACB中,∠ACB=45°,
∴AB=BC,
即:
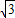 x+200=200
x+200=200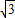 +x
+x∴x=200,∴AB=AE+BE=(200
 +200)米.
+200)米.点评:命题立意:此题主要考查解直角三角形的相关知识.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
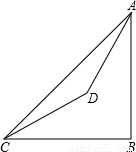
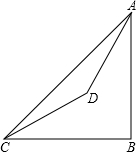 已知:如图,在山脚的C处测得山顶A的仰角为45°,沿着坡度为30°的斜坡前进400米到D处(即∠DCB=30°,CD=400米),测得A的仰角为60°,求山的高度AB.
已知:如图,在山脚的C处测得山顶A的仰角为45°,沿着坡度为30°的斜坡前进400米到D处(即∠DCB=30°,CD=400米),测得A的仰角为60°,求山的高度AB.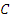 处测得山顶
处测得山顶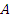 的仰角为
的仰角为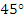 ,沿着坡角为
,沿着坡角为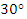 的斜坡前进
的斜坡前进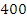 米到达
米到达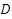 处(即∠
处(即∠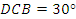 ,
, 米),测得
米),测得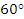 ,求山的高度
,求山的高度 .
.