Question

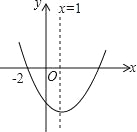
【题目】如图，抛物线y=ax2+c经过A（1，0），B（0，﹣2）两点．连结AB，过点A作AC⊥AB，交抛物线于点C．

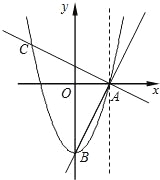
（1）求该抛物线的解析式；

（2）求点C的坐标；

（3）将抛物线沿着过A点且垂直于x轴的直线对折，再向上平移到某个位置后此抛物线与直线AB只有一个交点，请直接写出此交点的坐标．

Answer 1

【答案】（1）y=2x2﹣2；（2）（﹣，）；（3）（，3）．

【解析】

试题分析：（1）因为抛物线y=ax2+c经过A（1，0），B（0，﹣2）两点，则有：解得：，所求的抛物线的解析式是：y=2x2﹣2；

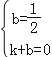（2）∵AC⊥AB，又根据题意可知：OA⊥BD，∴Rt△AOD∽Rt△BOA，∴，∴OD=，又根据A（1，0），B（0，﹣2），则有：AO=1，BO=2，∴OD=，∴D（0，），设直线AC的解析式是y=kx+b，则有，解得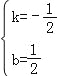：，∴所求的解析式是：y=﹣x+，由直线AC与抛物线y=2x2﹣2相交，则有：﹣x+=2x2﹣2，解得：x1=﹣，x2=1，当x=﹣时，y=﹣×（﹣）+=，∴点C的坐标是（﹣，）；

（3）抛物线沿着过A点且垂直于x轴的直线对折后与x轴的交点坐标为（1，0）和（3，0），此时抛物线解析式为y=2（x﹣2）2﹣2，向上平移此时解析式为y=2（x﹣2）2+k，直线AB的解析式为y=2x﹣2，则2（x﹣2）2+k=2x﹣2，△=100﹣80﹣8k=0，解得k=，即2（x﹣2）2+=2x﹣2，解得x=，所求交点的坐标是（，3）．