题目内容
已知:a和b都是无理数,且a≠b,下面提供的4个数a+b,a-b,ab,
,可能成为有理数的个数有
| a | b |
4
4
个.分析:利用特殊值法求解:当a=
,b=-
,a+b,ab,
都是有理数;当a=
,b=1+
,则a-b为有理数.
| 2 |
| 2 |
| a |
| b |
| 2 |
| 2 |
解答:解:当a=
,b=-
,则a+b=0,ab=-2,
=-1;
当a=
,b=1+
,则a-b=
-(1+
)=-1,
所以数a+b,a-b,ab,
都可能成为有理数.
故答案为4.
| 2 |
| 2 |
| a |
| b |
当a=
| 2 |
| 2 |
| 2 |
| 2 |
所以数a+b,a-b,ab,
| a |
| b |
故答案为4.
点评:本题考查了实数:有理数和无理数统称实数.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
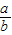 ,ab+a-b,ab+a+b可能成为有理数的个数有 个.
,ab+a-b,ab+a+b可能成为有理数的个数有 个.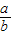 ,ab+a-b,ab+a+b可能成为有理数的个数有 个.
,ab+a-b,ab+a+b可能成为有理数的个数有 个.