��Ŀ����
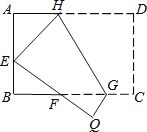
����Ŀ����ͼ��ֱ������ABCD�У�AB��CD����A=90�㣬AB=6��AD=4��DC=3������P�ӵ�A��������A��D��C��B�����ƶ�������Q�ӵ�A��������AB�����ƶ������P�ƶ���·��Ϊx����Q�ƶ���·��Ϊy���߶�PQƽ������ABCD���ܳ���
��1����y��x�ĺ�����ϵʽ�������x��y��ȡֵ��Χ��
��2����PQ��ACʱ����x��y��ֵ��
��3����P����BC����ʱ���߶�PQ�ܷ�ƽ������ABCD����������ܣ������ʱx��ֵ�������ܣ�˵�����ɣ�
���𰸡�
��1��
�⣺��C��CE��AB��E����CD=AE=3��CE=4���ɵ�BC=5��
��������ABCD���ܳ�Ϊ6+3+4+5=18��
��PQƽ��ABCD���ܳ���
��x+y=9��
��0��y��6��
��3��x��9��
�������ϵʽΪ��y=��x+9��3��x��9��

��2��
�⣺�����⣬Pֻ����BC���ϣ�7��x��9��
PB=12��x��BQ=6��y��
��ΪPQ��AC�����ԡ�BPQ�ס�BCA������ ![]() ��
��
�ã� ![]() ��
��
��6x��5y=42��
�ⷽ���� ![]()
�� ![]() ��
��
��3��
�⣺����ABCD�����Ϊ18��
��P����BC���ϣ���3��x��7��
a����3��x��4ʱ��P��AD���ϣ�S��APQ= ![]() xy��
xy��
����߶�PQ��ƽ������ABCD����������� ![]() ��
��
�ɵã� ![]() ��
��
��� ![]() ��
�� ![]() ����ȥ����
����ȥ����
b����4��x��7ʱ����P��DC���ϣ���ʱSADPQ= ![]() ��4��x��4+y����
��4��x��4+y����
����߶�PQ��ƽ������ABCD����������� ![]() ��4��x��4+y��=9��
��4��x��4+y��=9��
�ɵ� ![]() �˷������⣮
�˷������⣮
���Ե�x=3ʱ���߶�PQ��ƽ������ABCD�������

����������1����C��CE��AB��E���ɹ��ɶ������BC��ֵ�������õ����ε��ܳ�Ϊ18��������֪��y=��x+9�����ڵ�Qֻ��AB�ϣ�������ȷ����x��ȡֵ��Χ����2����PQ��AC�����BPQ�ס�BCA���� ![]() ����6x��5y=42����y=��x+9��ɷ�������⼴�ɣ���3��ͨ�����۵�P��λ�ã���������x��y�ķ��������x��ֵ��
����6x��5y=42����y=��x+9��ɷ�������⼴�ɣ���3��ͨ�����۵�P��λ�ã���������x��y�ķ��������x��ֵ��
�����㾫�������ý��Ԫһ�η�����ͺ�����ϵʽ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪��Ԫһ�η����飺�ٴ�����Ԫ�����ڼӼ���Ԫ����������ʾ������ϵ����ѧʽ�ӽ�����������ʽ������ϵʽ��