题目内容
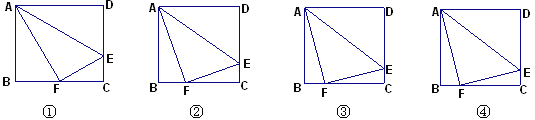
【题目】如图,点A(-1,0)、B(0,3)、C(2,4)、D(3,0),点P是x轴上一点,直线CP将四边形ABCD的面积分成1:2的两部分,则P点坐标为______.

【答案】P(![]() ,0)或(
,0)或(![]() ,0)
,0)
【解析】
作CE⊥x轴,根据四边形ABCD的面积=S△AOB+S梯形OBCE+S△CDE求得四边形的面积,设点P(x,0),则PD=3x,由直线CP将四边形ABCD的面积分成1:2两部分知S△CPD=3.5或S△CPD=7,据此列出方程求解可得.
过点C作CE⊥x轴于点E,
则AO=1、OB=3、OE=2、CE=4、DE=1,

∴四边形ABCD的面积=S△AOB+S梯形OBCE+S△CDE
=![]() ×1×3+
×1×3+![]() ×(3+4)×2+
×(3+4)×2+![]() ×1×4
×1×4
=10.5,
设点P(x,0),
则PD=3x,
由直线CP将四边形ABCD的面积分成1:2两部分知S△CPD=3.5或S△CPD=7,
则![]() ×(3x)×4=3.5或
×(3x)×4=3.5或![]() ×(3x)×4=7,
×(3x)×4=7,
解得:x=![]() 或x=
或x=![]() ,
,
即点P的坐标为(![]() ,0)或(
,0)或(![]() ,0),
,0),
故答案为:(![]() ,0)或(
,0)或(![]() ,0).
,0).

练习册系列答案
相关题目
【题目】某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完。设分配给甲店A型产品x件,两商店销售这两种产品每件的利润(元)如下表:
A型利润 | B型利润 | |
甲店 | 200 | 170 |
乙店 | 160 | 150 |
(1)分配给乙店B型产品 件(用含x的代数式表示)。
(2)设这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并直接写出x的取值范围。
(3)若公司要求总利润不低于17560元,有几种不同分配方案?哪种方案总利润最大?请求出最大利润。