题目内容
（2004•深圳）抛物线过点A（2，0）、B（6，0）、C（1，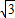
），平行于x轴的直线CD交抛物线于点C、D，以AB为直径的圆交直线CD于点E、F，则CE+FD的值是（ ）
A．2
B．4
C．5
D．6
【答案】分析：根据题意，G为直径AB的中点，连接GE，过G点作GH⊥CD于H．知CE+FD=CD-EF=CD-2EH，分别求出CD，EF即可．
解答：
解：由题意得：
D点坐标为（7，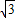
），
如图，G为直径AB的中点，连接GE，过G点作GH⊥CD于H．
则GH=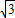
，EG=2，
则EH=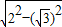
=1
∴CE+FD=CD-EF=CD-2EH=6-2=4．
故选B．
点评：此题首先要正确分析出各点的坐标，然后根据两点的坐标进行计算．
解答：
解：由题意得：D点坐标为（7，
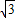），如图，G为直径AB的中点，连接GE，过G点作GH⊥CD于H．
则GH=
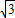，EG=2，则EH=
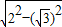=1∴CE+FD=CD-EF=CD-2EH=6-2=4．
故选B．
点评：此题首先要正确分析出各点的坐标，然后根据两点的坐标进行计算．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
（x+2）2+1的顶点坐标是（ ）
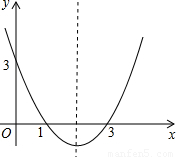
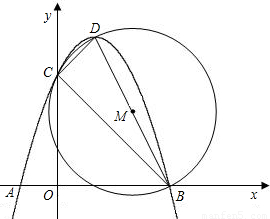
），平行于x轴的直线CD交抛物线于点C、D，以AB为直径的圆交直线CD于点E、F，则CE+FD的值是（ ）