题目内容
【题目】在边长为1的小正方形组成的方格纸中，若多边形的每个顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形.记格点多边形内的格点数为
，边界上的格点数为
，则格点多边形的面积可表示为
，其中
， 
为常数.
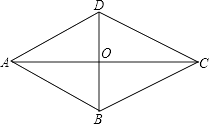
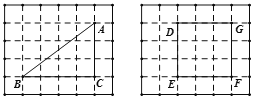
（1）在下面的两张方格纸中各有一个格点多边形，依次为
、正方形
.认真数一数： 
内的格点数是_______，正方形
边界上的格点数是_______;
（2）利用（1）中的两个格点多边形确定
， 
的值;
（3）现有一张方格纸共有110个格点，画有一个格点多边形，它的面积
，若该格点多边形外的格点数为
.
①填空：若
，则
＝ ；
②若
，求
的值．(写出解答过程)
【答案】（1）3，12；（2）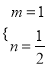
；（3）①18；②
＝7或8
【解析】试题分析：（1）利用格点图形的定义结合三角形以及正方形图形得出即可；
（2）利用已知图形，结合S=ma+nb-1得出关于m，n的关系式，进而求出即可；
（3）①由（2）知： 
，将S=40代入和a+b+c=110联立消去b即可求得a的值；②由
，用a 表示出b，由
用a表示出c，带入
，即可解得a的范围，由于a为整数，再确定出a的值即可.
试题解析：（1）由图可得： 
内的格点数是3，正方形DEFG边界上的格点数是12；
（2）：
面积为
×3×4=6，正方形DEFG面积为3×3=9，
依题意，得
，解得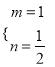
；
（3）①∵a是多边形内的格点数，b是多边形边界上的格点数，c是多边形外的格点数，总格点数为110，
∴a+b+c=110，
∵
,
∴a+2b =110,
由（2）知
，
∴
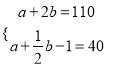,解得a=18.
故答案为：18；
②依题意，得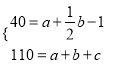
解得
代入
，得
解不等式组，得
∴整数
＝7或8.
练习册系列答案
相关题目
