题目内容
(2005•杭州)如图,在等腰Rt△ABC中,AC=BC,以斜边AB为一边作等边△ABD,使点C,D在AB的同侧;再以CD为一边作等边△CDE,使点C,E落在AD的异侧.若AE=1,则CD的长为( )
A.

B.

C.

D.

【答案】分析:在延长DC后,欲求DC,即DF-CF.而DF是直角三角形ADF的高,CF是等腰直角三角形ABC斜边上的高,根据题中条件,求出二者即可.
解答: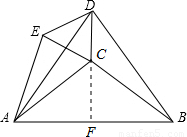 解:延长DC交AB于F
解:延长DC交AB于F
由题意易得,
∵AC=BC,
∴C在AB的垂直平分线上,
同理,D在AB的垂直平分线上,
∴CD是等边三角形ABD的角平分线,
所以∠ADC=30°,
则∠EDA=60°-30°=30°,
∵ED=DC,AD=AD,∠EDA=∠CDA=30°
∴△EDA≌△CDA
∴EA=AC=1
∴在等腰Rt△ABC中AB=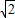
∴BF=CF=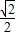 ,
,
在△ABD中tan∠BDF=tan30°=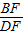 ,
,
∴DF=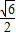 ,
,
∴DC=DF-CF=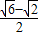 .
.
故选D.
点评:此题主要考查了等腰三角形、等边三角形和直角三角形的性质,综合利用了勾股定理和全等三角形的判定.
解答:
 解:延长DC交AB于F
解:延长DC交AB于F由题意易得,
∵AC=BC,
∴C在AB的垂直平分线上,
同理,D在AB的垂直平分线上,
∴CD是等边三角形ABD的角平分线,
所以∠ADC=30°,
则∠EDA=60°-30°=30°,
∵ED=DC,AD=AD,∠EDA=∠CDA=30°
∴△EDA≌△CDA
∴EA=AC=1
∴在等腰Rt△ABC中AB=
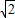
∴BF=CF=
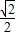 ,
,在△ABD中tan∠BDF=tan30°=
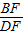 ,
,∴DF=
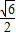 ,
,∴DC=DF-CF=
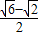 .
.故选D.
点评:此题主要考查了等腰三角形、等边三角形和直角三角形的性质,综合利用了勾股定理和全等三角形的判定.

练习册系列答案
相关题目



